重庆市沙坪坝区南渝中学校2022-2023学年八年级下学期数...

更新时间：2023-09-12 浏览次数：60 类型：月考试卷

一、单选题

1. (2023八下·沙坪坝月考) 下面图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024八下·琼海月考) 下列命题中不正确的是（）

A . 两组对角分别相等的四边形是平行四边形 B . 两组对边分别相等的四边形是平行四边形 C . 一组对边平行且相等的四边形是平行四边形 D . 对角线相等的四边形是平行四边形

答案解析收藏纠错 + 选题
3. (2024八下·琼海月考) 估算 $\text{[math]}$ 的结果（）

A . 在6和7之间 B . 在7和8之间 C . 在8和9之间 D . 在9和10之间

答案解析收藏纠错 + 选题
4. (2023八下·沙坪坝月考) 图，小颖依据所在城市2021年8月16日连续12个小时的风力变化情况，画出了风力随时间变化的图象，根据图象进行判断，下列说法正确的是（）

A . 8时风力最小 B . 在8时至12时，最大风力为5级 C . 风力在5级以上持续时间约为3.5小时 D . 8时至14时，风力不断增大

答案解析收藏纠错 + 选题
5. (2024八下·琼海月考) 代数式 $\text{[math]}$ 有意义，字母x的取值范围是（　　）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 且 $\text{[math]}$ D . $\text{[math]}$ 且 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八下·沙坪坝月考) 如图，直线y＝kx+b与直线y＝- $\text{[math]}$ 交于点A（m，2），则关于x的不等式kx+b $\text{[math]}$ x+ $\text{[math]}$ 的解集是（）

A . x≤2 B . x≥1 C . x≤1 D . x≥2

答案解析收藏纠错 + 选题
7. (2024九上·白云月考) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 没有实数根，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023八下·沙坪坝月考) 如图，菱形 $\text{[math]}$ 的对角线交于原点O，若点B的坐标为 $\text{[math]}$ ，点D的坐标为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 2 B . $\text{[math]}$ C . 6 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023八下·沙坪坝月考) 一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶，两车在途中相遇时，快车恰巧出现故障，慢车继续驶往甲地，快车维修好后按原速继续行驶乙地，两车到达各地终点后停止，两车之间的距离s（km）与慢车行驶的时间t（h）之间的关系如图.下列说法正确的是（）

A . 快车的速度为160km/h B . B点的坐标为 $\text{[math]}$ C . C点的坐标为 $\text{[math]}$ D . 慢车出发 $\text{[math]}$ 时两车相距200km

答案解析收藏纠错 + 选题
10. (2024八下·琼海月考) 已知一次函数 $\text{[math]}$ 的图象不经过第四象限，且关于 $\text{[math]}$ 的分式方程 $\text{[math]}$ 有整数解，则满足条件的所有整数 $\text{[math]}$ 的和为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024八下·琼海月考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2024七下·京口月考) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
13. (2024八下·琼海月考) 在平面直角坐标系中，若将抛物线 $\text{[math]}$ 先向右平移 $\text{[math]}$ 个单位长度，再向下平移 $\text{[math]}$ 个单位长度得到抛物线解析式为．

答案解析收藏纠错 + 选题
14. (2023八下·沙坪坝月考) 如图，在菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 相交于点O，点E是 $\text{[math]}$ 的中点．若 $\text{[math]}$ ， $\text{[math]}$ ，则菱形 $\text{[math]}$ 的面积为．

答案解析收藏纠错 + 选题
15. (2023八下·沙坪坝月考) 已知二次函数 $\text{[math]}$ ，当 $\text{[math]}$ 时，y的取值范围为.

答案解析收藏纠错 + 选题
16. (2023八下·沙坪坝月考) 若直线 $\text{[math]}$ ： $\text{[math]}$ 与直线 $\text{[math]}$ 经过 $\text{[math]}$ 轴上同一点，且 $\text{[math]}$ 与两坐标轴围成的三角形面积等于 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

17. (2024八下·琼海月考) 计算
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2023八下·沙坪坝月考) 先化简：若a是方程 $\text{[math]}$ 的解，求代数式 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
19. (2023八下·沙坪坝月考) 某市为庆祝二十大的召开，贯彻党的二十大精神，组织中学生举办了爱党知识竞赛．现随机抽取了部分学校的学生的测试成绩进行整理后（说明：测试成绩为x（分），分为5个等级，A等： $\text{[math]}$ ；B等： $\text{[math]}$ ；C等： $\text{[math]}$ ；D等： $\text{[math]}$ ；E等： $\text{[math]}$ ），绘制成如下不完整的条形统计图和扇形统计图，请结合统计图回答下列问题：
1. （1）在这次调查中，抽取的学生总人数是，C组对应的扇形圆心角的度数是；
2. （2）请补全条形统计图；
3. （3）某校现从A等级的4个学生中随机抽取2人去参加市赛，小明和小丽正好在这4个人当中，请用树状图法或列表法求小明和小丽都被抽到的概率是多少？
答案解析收藏纠错 + 选题
20. (2023八下·沙坪坝月考) 某电商在抖音上对种植成本为20元/千克的葡萄进行直播销售，如果按每千克40元销售，每天可卖出200千克.通过市场调查发现，如果该葡萄售价每千克降低1元，日销售量将增加20千克.
1. （1）若日利润保持不变，每千克该葡萄售价可降低多少元？
2. （2）老张的线下水果店也销售同款葡萄，标价为每千克50元.为提高市场竞争力，促进线下销售，老张决定对该葡萄实行打折销售，使其销售价格不超过（1）中的售价，则该商品至少需打几折销售？
答案解析收藏纠错 + 选题
21. (2023八下·沙坪坝月考) 如图，在平面直角坐标系中，直线 $\text{[math]}$ 经过点 $\text{[math]}$ 和点 $\text{[math]}$ ，与y轴交于点A，经过点C的另一直线与y轴的正半轴交于点 $\text{[math]}$ ，与x轴交于点E．
1. （1）求点A的坐标及直线 $\text{[math]}$ 的解析式；
2. （2）求四边形 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
22. (2023八下·安稳期中) 四边形 $\text{[math]}$ 为平行四边形，对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点O．
1. （1）用尺规完成以下基本作图：过点O作 $\text{[math]}$ 的垂线，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点E，F．（保留作图痕迹，不写作法，不下结论）
2. （2）在（1）问所作的图形中，连接 $\text{[math]}$ ， $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 为菱形．
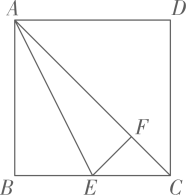
  证明：∵四边形ABCD为平行四边形
  ∴      ▲ ， $\text{[math]}$ ， $\text{[math]}$
  ∴ $\text{[math]}$
  在 $\text{[math]}$ 和 $\text{[math]}$ 中
        $\text{[math]}$
  ∴ $\text{[math]}$
  ∴      ▲
  ∵ $\text{[math]}$
  ∴四边形AFCE为平行四边形
  ∵       ▲
  ∴平行四边形AFCE为菱形
答案解析收藏纠错 + 选题

四、填空题

23. (2023八下·沙坪坝月考) 如图，正方形 $\text{[math]}$ ，点E、F、G、H分别在边 $\text{[math]}$ 上，若 $\text{[math]}$ 与 $\text{[math]}$ 的夹角为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长度为．

答案解析收藏纠错 + 选题
24. (2023八下·沙坪坝月考) 已知直线 $\text{[math]}$ 与 $\text{[math]}$ 轴的交点在A（2,0），B（3,0）之间（包括A、B两点）则 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
25. (2023八下·沙坪坝月考) 按顺序排列的若干个数： $\text{[math]}$ ，（ $\text{[math]}$ 是正整数），从第二个数 $\text{[math]}$ 开始，每一个数都等于1与它前面的那个数的差的倒数，即： $\text{[math]}$ ， $\text{[math]}$ ， ……，下列说法正确的个数有．
①若 $\text{[math]}$ ，则 $\text{[math]}$ ，

②若 $\text{[math]}$ ，则 $\text{[math]}$ ，

③若 $\text{[math]}$ ，则 $\text{[math]}$ ，

④当 $\text{[math]}$ 时，代数式 $\text{[math]}$ 的值恒为负．

答案解析收藏纠错 + 选题
26. (2024八下·埇桥月考) 若一个四位正整数 $\text{[math]}$ 满足： $\text{[math]}$ ，我们就称该数是“交替数”，则最小的“交替数”是；若一个“交替数”m满足千位数字与百位数字的平方差是15，且十位数字与个位数的和能被5整除．则满足条件的“交替数”m的最大值为．

答案解析收藏纠错 + 选题

五、解答题

27. (2023八下·沙坪坝月考) 小飞哥根据学习“一次函数”时积累的经验，对函数 $\text{[math]}$ 的图象与性质进行了探究，下面是小飞哥的探究过程，请补充完整：

（1）平面直角坐标系中，画出函数 $\text{[math]}$ 的图象：

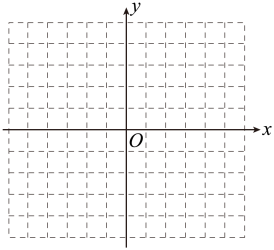
①在函数 $\text{[math]}$ 中，自变量的取值范围是；

②列表：

$\text{[math]}$	…	$\text{[math]}$	$\text{[math]}$	0	1	2	3	…
$\text{[math]}$	…	0	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	…

其中， $\text{[math]}$ ；

③描点、连线，在平面直角坐标系中，画出 $\text{[math]}$ 的图象；

（2）结合所画函数图象，写出 $\text{[math]}$ 两条不同类型的性质；
性质1：；
性质2：；
（3）小飞哥利用所画函数图象，估算不等式 $\text{[math]}$ 的解集是．

答案解析收藏纠错 + 选题

28. (2023八下·沙坪坝月考) 如图，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴， $\text{[math]}$ 轴分别交于 $\text{[math]}$ ， $\text{[math]}$ 两点，若将直线 $\text{[math]}$ 向右平移 $\text{[math]}$ 个单位得到直线 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 轴， $\text{[math]}$ 轴分别交于 $\text{[math]}$ ， $\text{[math]}$ 两点．
1. （1）求点 $\text{[math]}$ 的坐标；
2. （2）如图1，若点 $\text{[math]}$ 是直线 $\text{[math]}$ 上一动点，且 $\text{[math]}$ ， $\text{[math]}$ 轴，连接 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值及此时点 $\text{[math]}$ 的坐标；
3. （3）如图2，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，得到线段 $\text{[math]}$ ，延长线段 $\text{[math]}$ 得到直线 $\text{[math]}$ ，线段 $\text{[math]}$ 在直线 $\text{[math]}$ 上移动，当以点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 构成的三角形是等腰三角形时，直接写出点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
29. (2023八下·沙坪坝月考) 正方形 $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，连 $\text{[math]}$ ．
1. （1）如图，连 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的周长；
2. （2）如图，点 $\text{[math]}$ 在对角线 $\text{[math]}$ 上，满足 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上（不与端点重合），连接 $\text{[math]}$ ．若 $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）如图，在（1）的条件下， $\text{[math]}$ 是 $\text{[math]}$ 中点，点 $\text{[math]}$ 是直线 $\text{[math]}$ 上的一动点，连 $\text{[math]}$ ，将 $\text{[math]}$ 沿着 $\text{[math]}$ 翻折得到 $\text{[math]}$ ，连 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，连 $\text{[math]}$ 、 $\text{[math]}$ ，当 $\text{[math]}$ 的值最小时，请直接写出 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题