重庆市江北区第十八中学2022-2023学年八年级下学期数学...

更新时间：2023-08-28 浏览次数：44 类型：期中考试

一、单选题

1. (2023八下·江北期中) 下列计算中，正确的是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·南溪期中) 对于函数 $\text{[math]}$ ，下列结论正确的是（）．

A . 它的图像必经过点 $\text{[math]}$ B . 它的图像经过第一、二、三象限 C . 当 $\text{[math]}$ 时， $\text{[math]}$ D . y随x的增大而增大

答案解析收藏纠错 + 选题
3. (2023八下·江北期中) 下列条件中，可以判断四边形ABCD是平行四边形的是（）

A . 对角线互相垂直 B . 对角线相等 C . 一组对边平行且相等 D . 一组对边平行，另一组对边相等

答案解析收藏纠错 + 选题
4. (2023八下·江北期中) 在 $\text{[math]}$ 中，a，b，c分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的对边，若 $\text{[math]}$ ，则这个三角形一定是（）．

A . 等腰三角形 B . 直角三角形 C . 等腰直角三角形 D . 钝角三角形

答案解析收藏纠错 + 选题
5. (2023八上·阜南月考) 将一次函数 $\text{[math]}$ 与 $\text{[math]}$ 的图像画在同一坐标系中，正确的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2023八下·江北期中)
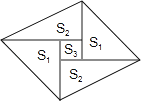
如图是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S₁ ，另两张直角三角形纸片的面积都为S₂ ，中间一张正方形纸片的面积为S₃ ，则这个平行四边形的面积一定可以表示为（）

A . 4S₁ B . 4S₂ C . 4S₂+S₃ D . 3S₁+4S₃

答案解析收藏纠错 + 选题
7. (2023八下·江北期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， D、E分别是 $\text{[math]}$ 的中点， F在 $\text{[math]}$ 延长线上，使 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则四边形 $\text{[math]}$ 的周长为（）．

A . 8 B . 9 C . 10 D . 11

答案解析收藏纠错 + 选题
8. (2023八下·江北期中) 一次函数y＝（a-7）x+a的图像不经过第三象限；且关于x的分式方程 $\text{[math]}$ 有整数解，则满足条件的整数a的和为（）

A . 18 B . 17 C . 12 D . 11

答案解析收藏纠错 + 选题
9. (2023八下·江北期中)
如图，点P是矩形ABCD的边AD上的一动点，矩形的两条边AB、BC的长分别是6和8，则点P到矩形的两条对角线AC和BD的距离之和是（　　）

A . 4.8 B . 5 C . 6 D . 7.2

答案解析收藏纠错 + 选题
10. (2023八下·江北期中) 已知正整数a，b，c，d满足 $\text{[math]}$ ，且 $\text{[math]}$ ，关于这个四元方程下列说法正确的个数是（）
① $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是该四元方程的一组解；
②连续的四个正整数一定是该四元方程的解；
③若 $\text{[math]}$ ，则该四元方程有21组解；
④若 $\text{[math]}$ ，则该四元方程有504组解．

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

11. (2023八下·江北期中) 代数式 $\text{[math]}$ 有意义，那么x的取值范围．

答案解析收藏纠错 + 选题
12. (2023八下·江北期中) 若6，11，m为三角形的三边长，则化简 $\text{[math]}$ 的结果为．

答案解析收藏纠错 + 选题
13. (2023八下·江北期中) 已知直线 $\text{[math]}$ 和 $\text{[math]}$ 图象上部分点的横坐标和纵坐标如下表所示，则关于x的方程 $\text{[math]}$ 的解是．
x
          $\text{[math]}$
0
1
2
          $\text{[math]}$
8
5
2
          $\text{[math]}$
          $\text{[math]}$
0
1
2
3

答案解析收藏纠错 + 选题
14. (2023八下·江北期中) 已知：如图，折叠长方形的一边 $\text{[math]}$ ，使点D落在 $\text{[math]}$ 边的点E处，已知 $\text{[math]}$ ，则 $\text{[math]}$ cm．

答案解析收藏纠错 + 选题
15. (2023八下·江北期中) 如图，点 $\text{[math]}$ 在平行四边形 $\text{[math]}$ 的边 $\text{[math]}$ 上， $\text{[math]}$ .若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
16. 在菱形ABCD中，∠A=30°，在同一平面内，以对角线BD为底边作顶角为120°的等腰三角形BDE，则∠EBC的度数为．

答案解析收藏纠错 + 选题
17. (2023八下·江北期中) 如图，在矩形ABCD中，AD=4，点P是直线AD上一动点，若满足△PBC是等腰三角形的点P有且只有3个，则AB的长为．

答案解析收藏纠错 + 选题
18. (2023八下·江北期中) 如果一个三位自然数t的各个数位上的数字均不为0，且满足个位数字与十位数字的和为9，百位数字与个位数字的和被6整除，那么称为“九六数”．把t的各个数位的和记为 $\text{[math]}$ ．若 $\text{[math]}$ （其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）是“九六数”，则满足条件的M中， $\text{[math]}$ 的最大的值为．

答案解析收藏纠错 + 选题

三、解答题

19. (2024八下·秀山期中) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2023八下·江北期中) 如图，已知平行四边形ABCD．
1. （1）用尺规完成以下基本作图：在CB的延长线上取点E，使CE＝CD，连接DE交AB于点F，作∠ABC的平分线BG交CD于点G．（保留作图痕迹，不写作法）
2. （2）在第（1）问所作的图形中，求证：四边形BFDG为平行四边形．
  证明：∵BG平分∠ABC
  ∴∠ABG＝∠CBG
  ∵四边形ABCD为平行四边形
  ∴AB∥CD
  ∴∠ABG＝∠CGB，∠CDE＝∠BFE
  ∴∠CGB＝       ▲
  ∴CB＝CG．
  ∵CE＝CD，CB＝CG
  ∴CE-CB＝CD-CG，即BE＝       ▲
  ∵CD＝CE
  ∴∠CDE＝       ▲
  ∵∠CDE＝∠BFE，∠CDE＝∠BEF
  ∴∠BFE＝       ▲
  ∴BE＝BF
  ∵BE＝DG，BE＝BF
  ∴DG＝       ▲
  ∵AB∥CD，DG＝BF
  ∴四边形BFDG为平行四边形．（  ）
答案解析收藏纠错 + 选题
21. (2023八下·南陵期末) 已知一次函数 $\text{[math]}$ （a是常数，且 $\text{[math]}$ ）．
1. （1）若该一次函数的图象与x轴相交于点 $\text{[math]}$ ，求一次函数的解析式．
2. （2）当 $\text{[math]}$ 时，函数有最大值5，求出此时a的值．
答案解析收藏纠错 + 选题
22. (2023八下·江北期中) 如图，在平行四边形 $\text{[math]}$ 中，点E、F分别为 $\text{[math]}$ 中点，G、H分别在边 $\text{[math]}$ 上，且 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是平行四边形；
2. （2）若 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是矩形．
答案解析收藏纠错 + 选题
23. (2023八下·江北期中) 问题：探究函数 $\text{[math]}$ 的图象与性质．
数学兴趣小组根据学习一次函数的经验，对函数 $\text{[math]}$ 的图象与性质进行了探究：
1. （1）在函数 $\text{[math]}$ ，自变量x可以是任意实数，下表是y与x的几组对应值：
  x
  …
            $\text{[math]}$
            $\text{[math]}$
            $\text{[math]}$
            $\text{[math]}$
  0
  1
  2
  3
  4
  …
  y
  3
  2
  1
  0
            $\text{[math]}$
            $\text{[math]}$
            $\text{[math]}$
  0
  a
  ①表格中a的值为；
  ②若 $\text{[math]}$ 为该函数图象上的点，则 $\text{[math]}$ ；
2. （2）在平面直角坐标系中，描出上表中的各点，画出该函数的图象；
3. （3）结合图象回答下列问题：
  ①当 $\text{[math]}$ 时，函数有最小值为；
  
  ②当自变量x满足什么条件时，函数值 $\text{[math]}$ ？
答案解析收藏纠错 + 选题
24. (2023八下·江北期中) 如图是一个滑梯示意图，若将滑梯 $\text{[math]}$ 水平放置，则刚好与DE一样长，已知滑梯的高度 $\text{[math]}$ 为3米， $\text{[math]}$ 为1米．
1. （1）求滑道 $\text{[math]}$ 的长度；
2. （2）若把滑梯 $\text{[math]}$ 改成滑梯 $\text{[math]}$ ，使 $\text{[math]}$ ，则求出 $\text{[math]}$ 的长．（精确到0.1米，参考数据： $\text{[math]}$ ）
答案解析收藏纠错 + 选题
25. (2023八下·江北期中) 阅读材料：小敏在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方．
例如：3＋2 $\text{[math]}$ ＝（1＋ $\text{[math]}$ ）² ，善于思考的小敏进行了以下探索：

当a、b、m、n均为整数时，若a＋b $\text{[math]}$ ＝（m＋n $\text{[math]}$ ）² ，则有a＋b $\text{[math]}$ ＝m²＋2n²＋2mn $\text{[math]}$ ．

a＝m²＋2n² ， b＝2mn．这样小敏就找到了一种把类似a＋b $\text{[math]}$ 的式子化为平方式的方法．

请你仿照小敏的方法探索并解决下列问题：
1. （1）当a、b、m、n均为整数时，若 $\text{[math]}$ ，用含mn的式子分别表示a、b，则：a＝　　， b＝　　；
2. （2）若a＋6 $\text{[math]}$ ＝（m＋n $\text{[math]}$ ）² ，且a、m、n均为正整数，求a的值；
3. （3）直接写出式子 $\text{[math]}$ 化简的结果．
答案解析收藏纠错 + 选题
26. (2023八下·江北期中) 在平行四边形ABCD中，连接BD，若BD⊥CD，点E为边AD上一点，连接CE，交BD于点F．
1. （1）如图1，若点E为AD中点，对角线AC与BD相交于点O，且△DFE的面积为 $\text{[math]}$ ， DF＝2，求CD的长；
2. （2）如图2，若点G在BD上，且DG＝AB，连接CG，过G作GH⊥CE于点H，连接DH并延长交AB于点M，若 $\text{[math]}$ ，用等式表示线段BM，DH，BD的数量关系，并证明；
3. （3）如图3，若∠ABC＝120°，AB＝2，点N在BC边上，BC＝4CN，且CE平分∠BCD，线段PQ（点P在点Q的左侧）在线段CE上运动，且 $\text{[math]}$ ，连接BP，NQ，请直接写出BP＋PQ＋QN的最小值．
答案解析收藏纠错 + 选题