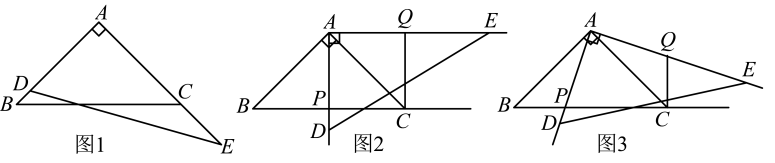
对于三人的答案,下列结论正确的是( )
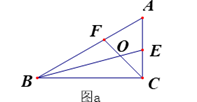
乐乐:如图 , 先在平地取一个可直接到达
,
的点
, 再连接
,
, 并分别延长
至
,
至
, 使
,
, 最后测出
的长即为
,
的距离.
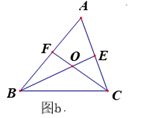
明明:如图 , 先过点
作
的垂线
, 再在
上取
,
两点,使
, 接着过点
作
的垂线
, 交
的延长线于点
, 则测出
的长即为
,
的距离.
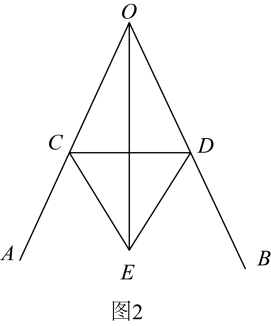
聪聪:如图 , 过点
作
, 再由点
观测,在
的延长线上取一点
, 使
这时只要测出
的长即为
,
的距离.
以上三位同学所设计的方案中可行的是( )




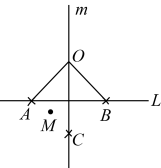
请写出平分
的依据:;

小明根据以上信息研究发现:不一定必须是等边三角形,只需
即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在
的边
,
上分别取
, 移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线
是
的平分线,请说明此做法的理由;

小明将研究应用于实践.如图4,校园的两条小路和
, 汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
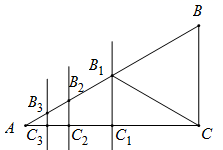
【问题背景】如图1,一副三角板的直角顶点重合,两条直角边分别共线,将它们分别记作 ,
. 其中
,
,
,
. 现固定三角板
, 将三角板
绕点A逆时针旋转,旋转角记为
, 射线
与射线
交于点P,在射线
上取一点Q,使
, 连接CQ.