山西省吕梁市中阳县2022-2023学年八年级下学期期末数学...

更新时间：2023-09-14 浏览次数：34 类型：期末考试

一、单选题

1. (2023八下·中阳期末) 下列函数中， $\text{[math]}$ 是 $\text{[math]}$ 的一次函数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八下·中阳期末) 下列各式计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023八下·中阳期末) 直角三角形的三边长分别为3，4，x，则 $\text{[math]}$ 的值可能为（）

A . 5 B . $\text{[math]}$ C . 7 D . 5或 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八下·中阳期末) 在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八下·中阳期末) 八年级（1）班的期末综合成绩按照课堂表现、作业成绩、考试成绩2：3：5的比例计算，小明的课堂表现为80分，作业成绩为90分，考试成绩为85分，那么小明的期末综合成绩为（）

A . 85分 B . 85.5分 C . 86分 D . 86.5分

答案解析收藏纠错 + 选题
6. (2023九上·杭州开学考) 如图，菱形 $\text{[math]}$ 中， $\text{[math]}$ 分别是 $\text{[math]}$ 的中点，若菱形 $\text{[math]}$ 的周长为 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023八下·中阳期末) 一次函数 $\text{[math]}$ 的图像如图所示，当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023八下·中阳期末) 如图所示的是丽丽家正方形后院的示意图，丽丽家打算在正方形后院打造一个 $\text{[math]}$ 的正方形游泳池和一个 $\text{[math]}$ 的正方形花园，剩下阴影部分铺满瓷砖，则阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023八下·中阳期末) 已知小明家、体育馆、图书馆依次在同一条直线上．小明从家出发，匀速骑行到达体育馆；在体育馆停留一段时间后，匀速步行到达图书馆；在图书馆停留一段时间后，匀速骑行返回家中．给出的图象反映了这个过程中小明离开家的距离 $\text{[math]}$ 与离开家的时间 $\text{[math]}$ 之间的对应关系．下列说法不正确是（）

A . 体育馆与图书馆之间的距离为 $\text{[math]}$ B . 小明从体育馆到图书馆的步行速度为 $\text{[math]}$ C . 小明在体育馆停留了 $\text{[math]}$ 分钟 D . 小明从家去体育馆的速度比从图书馆回家的速度快

答案解析收藏纠错 + 选题
10. (2023八上·梧州期中) 小明用相同的积木玩一个拼图游戏，该积木每个角都是直角，长度如图1所示，小明用 $\text{[math]}$ 个这样的积木，按照如图2所示的方法玩拼图游戏，两两相扣，相互间不留空隙．则图形的总长度 $\text{[math]}$ 与图形个数 $\text{[math]}$ 之间的关系式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023八下·中阳期末) 若 $\text{[math]}$ 在实数范围内有意义，则实数 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
12. (2023八下·中阳期末) 如图所示的是甲、乙两公司上半年前5个月利润的折线统计图，则 $\text{[math]}$ $\text{[math]}$ （填“>”或“<”）．

答案解析收藏纠错 + 选题
13. (2023八下·中阳期末) 将直线 $\text{[math]}$ 向右平移3个单位长度后与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为．

答案解析收藏纠错 + 选题
14. (2023八下·中阳期末) 攀岩是一项在天然岩壁或人工岩壁上进行的向上攀爬的运动项目．如图，攀岩墙近似一个长方体的两个侧面，小天根据学过的数学知识准确地判断出从点 $\text{[math]}$ 攀爬到点 $\text{[math]}$ 的最短路径为米．

答案解析收藏纠错 + 选题
15. (2023八下·中阳期末) 在平面直角坐标系中，一次函数 $\text{[math]}$ 的图像分别交 $\text{[math]}$ 轴， $\text{[math]}$ 轴于B，C两点，点A坐标为 $\text{[math]}$ ，直线 $\text{[math]}$ 上有一点 $\text{[math]}$ ，使得 $\text{[math]}$ 是以点A为直角顶点的等腰直角三角形，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

16. (2023八下·中阳期末)
1. （1）计算： $\text{[math]}$ ．
2. （2）下面是小华同学解答题目的过程，请认真阅读并完成相应任务．
  计算： $\text{[math]}$ ．
  解：原式 $\text{[math]}$ 第一步
        $\text{[math]}$ 第二步
        $\text{[math]}$ 第三步
  任务一：以上步骤中，从第    ▲        步开始出现错误，这一步错误的原因是    ▲         ．
  任务二：请写出正确的计算过程．
答案解析收藏纠错 + 选题
17. (2023八下·中阳期末) 如图， $\text{[math]}$ 是菱形 $\text{[math]}$ 对角线的交点，过点 $\text{[math]}$ 作 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ． $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ．求证：四边形 $\text{[math]}$ 是矩形．

答案解析收藏纠错 + 选题

18. (2023八下·中阳期末) 为了解学生对五一劳动节上映的《长空之王》与《灌篮高手》两部电影的评价，某调查小组从该校八年级中随机抽取了20名学生对这两部作品分别进行打分（满分10分），并进行整理、描述和分析，下面给出了部分信息．

《长空之王》得分情况：7，8，7，10，7，6，9，9，10，10，8，9，8，6，6，10，9，7，9，9．

《灌篮高手》的得分统计图：

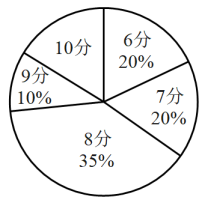
抽取的学生对两部作品分别打分的平均数，众数和中位数：

	平均数	众数	中位数
《长空之王》	8.2	$\text{[math]}$	8.5
《灌篮高手》	7.8	8	$\text{[math]}$

根据以上信息，解答下列问题：

（1）上述图表中的 $\text{[math]}$ ， $\text{[math]}$ ．
（2）根据上述数据，你认为该校八年级学生对哪部作品评价更高？请说明理由（写出一条理由即可）．

答案解析收藏纠错 + 选题

19. (2023八下·中阳期末) 已知一次函数的图象与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴正半轴相交于点 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求该一次函数的解析式．
2. （2）若点 $\text{[math]}$ 和点 $\text{[math]}$ 在该一次函数的图象上，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
20. (2023八下·中阳期末) 甲、乙两根蜡烛燃烧时剩余部分的高度 $\text{[math]}$ 与燃烧时间 $\text{[math]}$ 之间的关系如图所示，已知 $\text{[math]}$ ，请根据所提供的信息解答下列问题：
1. （1）乙蜡烛燃烧前的高度是 $\text{[math]}$ ，乙从点燃到燃尽所用的时间是 $\text{[math]}$ ．
2. （2）燃烧多长时间时，甲、乙两根蜡烛的高度一样长？
答案解析收藏纠错 + 选题
21. (2023八下·中阳期末) 阅读与思考
请你阅读下列材料，并完成相应的任务．

裂项法，是数学中求和的一种方法，是分解与组合思想在求和中的具体应用．具体方法是将求和中的每一项进行分解，然后重新组合，使之能消去一些项，最终达到求和的目的．我们以往的学习中已经接触过分数裂项求和．例如： $\text{[math]}$ ．

在学习完二次根式后我们又掌握了一种根式裂项．例如： $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）模仿材料中的计算方法，化简： $\text{[math]}$ ．
2. （2）观察上面的计算过程，直接写出式子 $\text{[math]}$ ．
3. （3）利用根式裂项求解： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2023八下·中阳期末) 综合与实践
问题情境：在数学活动课上，数学老师让同学们用一张矩形纸片进行探究活动．

小亮准备了矩形纸片 $\text{[math]}$ ，其中 $\text{[math]}$ 是 $\text{[math]}$ 的中点，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 的对应点为 $\text{[math]}$ ．
1. （1）观察发现：如图1，当点 $\text{[math]}$ 恰好在 $\text{[math]}$ 边上时，小亮发现 $\text{[math]}$ 与 $\text{[math]}$ 存在一定的数量关系，其数量关系是．
2. （2）探索猜想：如图2，当点 $\text{[math]}$ 在矩形 $\text{[math]}$ 内部时，延长 $\text{[math]}$ 交 $\text{[math]}$ 边于点 $\text{[math]}$ ．试猜想线段 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系，并说明理由．
3. （3）拓展延伸：当点 $\text{[math]}$ 在矩形 $\text{[math]}$ 内部时，若 $\text{[math]}$ ，直接写出线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系．
答案解析收藏纠错 + 选题
23. (2023八下·中阳期末) 综合与探究
如图，直线 $\text{[math]}$ 分别交 $\text{[math]}$ 轴， $\text{[math]}$ 轴于点 $\text{[math]}$ ，过点A作直线 $\text{[math]}$ 分别交 $\text{[math]}$ 轴， $\text{[math]}$ 轴于点 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求直线 $\text{[math]}$ 的解析式．
2. （2）在 $\text{[math]}$ 轴左侧作直线 $\text{[math]}$ 轴，分别交直线 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ．当 $\text{[math]}$ 时，过点 $\text{[math]}$ 作直线 $\text{[math]}$ $\text{[math]}$ 轴，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ．能否在直线 $\text{[math]}$ 上找一点 $\text{[math]}$ ，使 $\text{[math]}$ 的值最小，求出 $\text{[math]}$ 点的坐标．
3. （3） $\text{[math]}$ 为直线 $\text{[math]}$ 上一点，在（2）的条件下， $\text{[math]}$ 轴上是否存在点 $\text{[math]}$ 使得以 $\text{[math]}$ 为顶点的四边形为平行四边形？若存在，请直接写出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题