 B .
B .  C .
C .  D .
D . 
 B .
B . 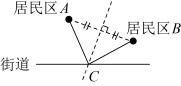 C .
C . 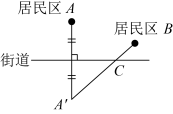 D .
D . 

 B .
B .  C .
C .  D .
D . 


请你根据统计图提供的信息,回答下列问题:
①估计这批花卉成活的棵树;
②根据市政规划共需要成活90000棵这种花卉,估计还需要移植多少棵?


下面是小明同学的数学学习笔记,请您仔细阅读并完成相应的任务:构造全等三角形解决图形与几何问题
在图形与几何的学习中,常常会遇到一些问题无法直接解答,需要添加辅助线才能解决.比如下面的题目中出现了角平分线和垂线段,我们可以通过延长垂线段与三角形的一边相交构造全等三角形,运用全等三角形的性质解决问题.
例:如图1,是
内一点,且
平分
,
, 连接
, 若
的面积为10,求
的面积.

该问题的解答过程如下:
解:如图2,过点作
交
延长线于点
,
、
交于点
,

平分
,
.
,
.
在和
中,
,
(依据1)
(依据2),
,
,
.
……



如图1,中,
,
, 点C在直线l上,点A、B在直线l的同侧,过点A作
于点D.
如图1,在直线l上取点E,使 . 则
与
的数量关系是,此时
、
、
之间的数量关系是.
如图2,在直线l上取点F,使 , 猜想
与
的数量关系,并说明理由(辅助线提示:过点B作
于点H)
在直线l任取一点P,连接 , 以点P为直角顶点作等腰直角三角形
, 作
于点N,请分别探索在图3,图4中
、
、
之间的数量关系,直接写出答案.