广东省肇庆市端州区校2023-2024学年高二上册数学开学适...

更新时间：2023-11-17 浏览次数：47 类型：开学考试

一、单选题（本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。）

1. (2024高二上·汉川期中) 复数 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高二上·铜梁月考) 甲、乙同时参加某次法语考试，甲、乙考试达到优秀的概率分别为0.6，0.7，两人考试相互独立，则甲、乙两人都未达到优秀的概率为（）

A . 0.42 B . 0.12 C . 0.18 D . 0.28

答案解析收藏纠错 + 选题
3. (2023高二上·端州开学考) 若一组样本数据 $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ 的方差为0.01，则数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ 的方差为（）

A . 0.04 B . 1.16 C . 0.16 D . 1.04

答案解析收藏纠错 + 选题
4. (2023高二上·端州开学考) 在 $\text{[math]}$ 中，角A ， B ， C的对边分别是a ， b ， c ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 6 B . 7 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023高二上·端州开学考) 已知点 $\text{[math]}$ 关于y轴的对称点为B ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023高二上·端州开学考) P是 $\text{[math]}$ 所在平面内一点，若 $\text{[math]}$ ，其中 $\text{[math]}$ ，则点P一定在（）

A . $\text{[math]}$ 内部 B . AC边所在的直线上 C . AB边所在的直线上 D . BC边所在的直线上

答案解析收藏纠错 + 选题
7. (2023高二上·端州开学考) 已知向量 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，则实数k的值为（）

A . $\text{[math]}$ B . 0 C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023高二上·端州开学考) 某校有年轻教师30人和老教师20人进行党史答题比赛．按照分层抽样的方法抽取5名教师，相关统计情况如下：年轻教师答对题目的平均数为2，方差为0.5；老教师答对题目的平均数为3，方差为1，则这5人答对题目的方差为（）

A . 0.61 B . 0.675 C . 0.74 D . 0.94

答案解析收藏纠错 + 选题

二、多选题（本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分．）

9. (2023高二上·端州开学考) 投掷一枚质地均匀的正方体骰子，下列说法正确的有（）

A . “出现点数为奇数”的概率等于“出现点数为偶数”的概率” B . 只要连掷6次，一定会“出现1点” C . 投掷前默念几次“出现6点”，投掷结果“出现6点”的可能性就会加大 D . 连续投掷3次，出现的点数之和不可能等于19

答案解析收藏纠错 + 选题
10. (2023高二上·端州开学考) 已知a ， b ， c为 $\text{[math]}$ 的三内角A、B、C的对边，下列命题中正确的是（）

A . 在 $\text{[math]}$ 中， $\text{[math]}$ 的充要条件是 $\text{[math]}$ B . 在锐角 $\text{[math]}$ 中，不等式 $\text{[math]}$ 恒成立 C . 在 $\text{[math]}$ 中，若 $\text{[math]}$ ，则 $\text{[math]}$ 必是等腰直角三角形 D . 在 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 必是等边三角形

答案解析收藏纠错 + 选题
11. (2023高二上·端州开学考) 函数 $\text{[math]}$ 在一个周期内的图像如图所示，则（）

A . 该函数的解析式为 $\text{[math]}$ B . 该函数图象的对称中心为 $\text{[math]}$ ， $\text{[math]}$ C . 该函数的增区间是 $\text{[math]}$ ， $\text{[math]}$ D . 把函数 $\text{[math]}$ 的图像上所有点的横坐标伸长为原来的 $\text{[math]}$ 倍，纵坐标不变，可得到该函数图象

答案解析收藏纠错 + 选题
12. (2023高二上·端州开学考) 《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”；底面为矩形，一条侧棱垂直于底面的四棱锥称为“阳马”，四个面均为直角三角形的四面体称为“鳖臑”，如图在堑堵 $\text{[math]}$ 中， $\text{[math]}$ ，且 $\text{[math]}$ ．下列说法正确的是（）

A . 四棱锥 $\text{[math]}$ 为“阳马” B . 四面体 $\text{[math]}$ 为“鳖臑” C . M为线段 $\text{[math]}$ 上的动点，则AM与BC所成角的大小恒为60° D . 过A点分别作 $\text{[math]}$ 于点E ， $\text{[math]}$ 于点F ，则 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题（本大题共4小题，每小题5分）

13. (2023高二上·端州开学考) 设向量 $\text{[math]}$ 绕点O逆时针旋转 $\text{[math]}$ 得向量 $\text{[math]}$ ，且 $\text{[math]}$ ，则向量 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2023高二上·端州开学考) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的面积为．

答案解析收藏纠错 + 选题
15. (2024高三上·绵竹月考) 已知圆台的下底面半径为6，上底面半径为3，其侧面积等于上、下底面积之和，则圆台的高为．

答案解析收藏纠错 + 选题
16. (2023高二上·端州开学考) 如图，平行六面体 $\text{[math]}$ 中，各条棱长均为1，共顶点A的三条棱两两所成的角均为60°，则对角线 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

四、解答题（本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤．）

17. (2024高二上·斗门月考) 某项选拔共有三轮考核，每轮设有一个问题，能正确回答问题者进入下一轮，否则被淘汰．已知甲选手能正确回答第一、二、三轮的问题的概率分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，乙选手能正确回答第一、二、三轮的问题的概率分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且两位选手各轮问题能否正确回答互不影响．
1. （1）求甲选手进入第三轮才被淘汰的概率；
2. （2）求至少有一名选手通过全部考核的概率．
答案解析收藏纠错 + 选题
18. (2023高二上·端州开学考) 为响应商务部“2023消费提振年”、“百城联动”汽车节和“千县万镇”新能源汽车消费季活动，西安市相关部门为了解现有的新能源汽车充电设备的覆盖和使用情况，随机选取了100名新能源汽车车主进行问卷调查，并将问卷中的这100人根据其满意度评分值（满分100）按照 $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ 分成5组，制成频率分布直方图如图所示．
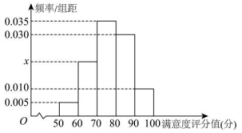
1. （1）求频率分布直方图中x的值；
2. （2）估计这组数据的众数、平均数和中位数．
答案解析收藏纠错 + 选题
19. (2023高二上·端州开学考) 已知函数 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的最小正周期、对称中心和 $\text{[math]}$ 的单调递减区间；
2. （2）当 $\text{[math]}$ 时，求函数 $\text{[math]}$ 的最小值及取得最小值时x的值．
答案解析收藏纠错 + 选题
20. (2023高二上·端州开学考) 如图所示，平面 $\text{[math]}$ 平面ABCD ，四边形AEFB为矩形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求多面体ABCDEF的体积；
2. （2）求二面角F-CD-A的余弦值．
答案解析收藏纠错 + 选题
21. (2023高二上·端州开学考) 记钝角 $\text{[math]}$ 的内角A ， B ， C的对边分别为a ， b ， c ，已知 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求A；
2. （2）求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
22. (2023高二上·端州开学考) 如图，在矩形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， M是线段AD上的一动点，将 $\text{[math]}$ 沿着BM折起，使点A到达点A＇的位置，满足点 $\text{[math]}$ 平面BCDM且点A＇在平面BCDM内的射影E落在线段BC上．
1. （1）当点M与端点D重合时，证明： $\text{[math]}$ 平面ACD＇；
2. （2）求三棱锥E-A＇BM的体积的最大值；
3. （3）设直线CD与平面A＇BM所成的角为 $\text{[math]}$ ，二面角A＇-BM-C的平面角为 $\text{[math]}$ ，求 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题