 B .
B .  C .
C .  D .
D . 

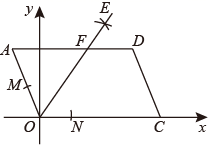
①以点O为圆心,适当长为半径画弧,分别交 于点M , 交
于点N . ②分别以点M , N为圆心,大于
的长为半径画弧,两弧在
内相交于点E . ③画射线
,交
于点
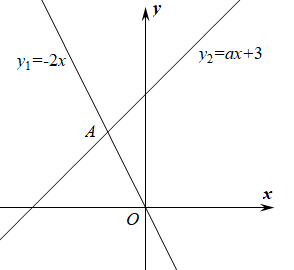
,则点A的坐标为( )
|
|
甲商品 |
乙商品 |
|
进价(元/件) |
65 |
5 |
|
售价(元/件) |
90 |
10 |
小华计划购进甲、乙商品共100件进行销售,设小华购进甲商品x件.
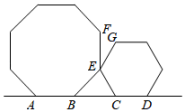
小云同学是这么做的:延长至
, 使得
, 连
, 可证明
, 得到
是等腰直角三角形,由此证明出
平分
, 还可以知道
三者关系为: ;
