重庆市2023年中考模拟数学考试试卷

更新时间：2023-10-24 浏览次数：56 类型：中考模拟

一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑。

1. (2023·重庆市模拟) 下列四个实数中，是负数的是（　　）

A . -（-1） B . （-1）²⁰²² C . |-1| D . （-1）²⁰²³

答案解析收藏纠错 + 选题
2. (2023·重庆市模拟) 单项式-5ab³的系数是（　　）

A . 5 B . -5 C . 4 D . 3

答案解析收藏纠错 + 选题
3. (2023·重庆市模拟) 某几何体的三视图如图所示，该几何体是（　　）

A . 三棱柱 B . 正方体 C . 圆锥 D . 圆柱

答案解析收藏纠错 + 选题
4. (2023·重庆市模拟) 若m＞n ，则下列不等式中正确的是（　　）

A . m-2＜n-2 B . $\text{[math]}$ m $\text{[math]}$ n C . n-m＞0 D . 1-2m＜1-2n

答案解析收藏纠错 + 选题
5. (2023·重庆市模拟) 在平面直角坐标系中，有两个点A（2，3），B（3，4），若反比例函数y $\text{[math]}$ 的图象与线段AB有交点，则k的值可能是（　　）

A . -8 B . 7 C . 13 D . 2023

答案解析收藏纠错 + 选题
6. (2023·重庆市模拟) 将一些完全相同的棋子按如图所示的规律摆放，第①个图中有4颗棋子，第②个图中有7颗棋子，第③个图中有12颗棋子，…，按此规律，则第⑧个图中棋子的颗数是（　　）

A . 32 B . 52 C . 67 D . 84

答案解析收藏纠错 + 选题
7. (2023·重庆市模拟) 下列计算正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ = $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ = $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023·重庆市模拟) 如图，AB是⊙O的直径，点C ， D在⊙O上，连接CD ，若∠BAD＝72°，则∠C＝（　　）

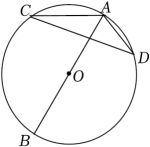
A . 36° B . 28° C . 15° D . 18°

答案解析收藏纠错 + 选题
9. (2023·重庆市模拟) 如图，矩形ABCD的对角线AC的垂直平分线分别交AD、AC、BC于点E、O、F ，若AB＝12，BC＝16，则EF的长为（　　）

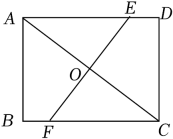
A . 8 B . 15 C . 16 D . 24

答案解析收藏纠错 + 选题
10. (2023·重庆市模拟) 一个正整数等于两个不相等的正整数的和与这两个不相等的正整数的积之和，称这个整数为“可拆分”整数，反之则称“不可拆分”整数.例如， $\text{[math]}$ ， 11是一个“可拆分”整数.下列说法：
①最小的“可拆分”整数是5；
②一个“可拆分”整数的拆分方式可以不只有一种；
③最大的“不可拆分”的两位整数是96.
其中正确的个数是（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题

二、填空题（本大题8个小题，每小题4分，共32分）请将每小题的答案直接填在答题卡中对应的横线上。

11. (2023·重庆市模拟) 计算：9tan30° $\text{[math]}$ 3^-²＝．

答案解析收藏纠错 + 选题
12. (2023·重庆市模拟) 已知一元二次方程kx²﹣9x+8=0的一个根为1，则k的值为．

答案解析收藏纠错 + 选题
13. (2023·重庆市模拟) 已知y $\text{[math]}$ 2 $\text{[math]}$ 2．那么x＝．

答案解析收藏纠错 + 选题
14. (2024九下·杨浦模拟) 在四张完全相同的卡片上，分别画有：正三角形、正八边形、圆和矩形．如果从中任意抽取1张卡片，那么这张卡片上所画图形既是轴对称图形又是中心对称图形的概率是．

答案解析收藏纠错 + 选题
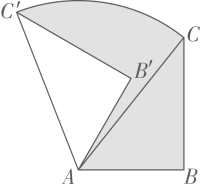
15. (2023·重庆市模拟) 如图，在Rt△ABC中，∠B＝90°，AB＝2，BC＝3，将Rt△ABC绕点A逆时针旋转60°后得到△AB'C'，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
16. (2023·重庆市模拟) 关于x的二次函数y＝-x²+（a-3）x-1在y轴的左侧，y随x的增大而增大，且使得x的分式方程 $\text{[math]}$ 1 $\text{[math]}$ 有整数解的整数a值为．

答案解析收藏纠错 + 选题
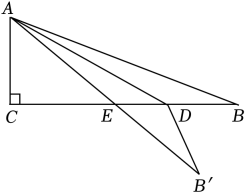
17. (2023·重庆市模拟) 如图，在Rt△ABC的纸片中，∠C＝90°，AC＝7，AB＝25，点D在边BC上，以AD为折痕将△ADB折叠得到△ADB′，AB′与边BC交于点E ．若△EDB′为直角三角形，则BD的长是．

答案解析收藏纠错 + 选题
18. (2023·重庆市模拟) 若一个四位正整数 $\text{[math]}$ 满足： $\text{[math]}$ ，我们就称该数是“交替数” $\text{[math]}$ 若一个“交替数” $\text{[math]}$ 满足千位数字与百位数字的平方差是 $\text{[math]}$ ，且十位数字与个位数字的和能被 $\text{[math]}$ 整除，则满足条件的 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题

三、解答题（本大题共8个小题，19题8分，20-26每小题10分，共78分）解答题时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括作辅助线），请将解答过程书写在答题卡中对应的位置上。

19. (2023·重庆市模拟) 化简：
1. （1） 5x（1+x）-（x-2）（5x+1）
2. （2） $\text{[math]}$ （x-2 $\text{[math]}$ ）
答案解析收藏纠错 + 选题
20. (2023·重庆市模拟) 如图，在△ABC中，AB＝AC ，过点A作AD⊥BC交BC于点D ．点E是线段AD上一点，连接BE ，请完成下面的作图和填空．
1. （1）用尺规完成以下基本作图：以点C为顶点，在BC的右边作∠BCF＝∠EBD ，射线CF交AD的延长线于点F ，连接BF ， EC ．（保留作图痕迹，不写作法，不下结论）
2. （2）利用对角线互相垂直的平行四边形是菱形，求证：四边形BECF是菱形．
  证明：∵AB＝AC ， AD⊥BC ，
  ∴①     ▲     ，
  ∴BE＝CE ．
  在△BED和△CFD中， $\text{[math]}$ ，
  ∴△BED≌△CFD ，
  ∴③     ▲  ．
  ∴四边形BECF是平行四边形．
  ∵④     ▲  ，
  ∴四边形BECF是菱形．
答案解析收藏纠错 + 选题
21. (2023·重庆市模拟) 为了解出租车司机的收入情况，某校七年级数学兴趣小组从甲、乙两家出租车公司分别随机抽取10名司机的月收入（单位：千元）进行统计，其情况如表：
甲公司司机月收入情况

月收入（千元）
4
5
6
7
8
人数（名）
1
2
4
2
1
乙公司司机月收入情况

月收入（千元）
4
5
9
12
人数（名）
5
2
2
1
根据以上信息，整理分析数据如表：


平均数
中位数
众数
甲公司司机月收入（千元）
6
a
b
乙公司司机月收入（千元）
c
d
4
1. （1）填空：a＝，b＝，c＝，d＝；
2. （2）若甲公司将出租车换成新能源汽车，运营成本下降，每个司机的月收入都增加了1千元，则甲公司司机月收入的方差会（填“变大”，“变小”或“不变”）；
3. （3）某人决定从两家公司中选择一家应聘出租车司机，你建议他选哪家公司？简述理由．
答案解析收藏纠错 + 选题
22. (2023·汨罗一模) 某健身器材店计划购买一批篮球和排球，已知每个篮球进价是每个排球进价的1.5倍，若用3600元购进篮球的数量比用3200元购进排球的数量少10个．
1. （1）篮球、排球的进价分别为每个多少元?
2. （2）该健身器材店决定用不多于28000元购进篮球和排球共300个进行销售，最多可以购买多少个篮球?
答案解析收藏纠错 + 选题
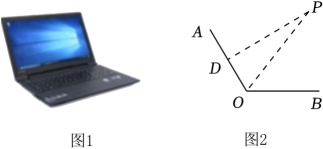
23. (2023·重庆市模拟) 如图1是一台置于水平桌面上的笔记本电脑，忽略其厚度，将结构简化成图2，其外部结构由显示屏OA、键盘和触摸板OB两大部分组成，OA＝OB＝30cm ．
1. （1）打开电脑时，若∠AOB＝120°，求点A到桌面的距离；
2. （2）若D为OA的中点，测得电脑使用者的眼睛所在位置P到D点距离PD＝36cm ，且∠PDO＝90°，求O ， P两点之间的距离．（参考数据： $\text{[math]}$ ，结果保留一位小数）
答案解析收藏纠错 + 选题
24. (2023·重庆市模拟)
1. （1）由“函数与方程关系”可知：方程x+2 $\text{[math]}$ （可化为x²+2x-1＝0）的解，可看作函数y＝x+2的图象与函数y $\text{[math]}$ 的图象交点的横坐标，则方程kx²+x-4＝0（k≠0）的两个解，可看作直线y＝与双曲线y $\text{[math]}$ 交点的横坐标；
2. （2）若直线y＝kx+b与双曲线y $\text{[math]}$ （k＞0）交于（-1，m），（2，n），求不等式kx+b $\text{[math]}$ 的解．
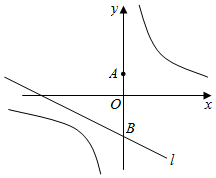
3. （3）若点A的坐标是（0，1），直线l：y $\text{[math]}$ x-2与y轴交于点B ，点C是直线l上一动点，过点C作x轴的垂线，交双曲线y $\text{[math]}$ 于D ，若A ， B ， C ， D四点是一个平行四边形的四个顶点，求D的坐标．
答案解析收藏纠错 + 选题
25. (2023·重庆市模拟) 定义：对于一次函数y＝kx+m（k ， m是常数，k≠0）和二次函数y＝ax²+bx+c（a ， b ， c是常数，a≠0），如果k＝2a ， m＝b ，那么y＝kx+m叫做y＝ax²+bx+c的牵引函数．
1. （1）直接写出 $\text{[math]}$ 的牵引函数；
2. （2）若二次函数 $\text{[math]}$ （a是常数，a≠0）的图象与其牵引函数的图象有且只有一个交点，求a的值；
3. （3）若点P为二次函数 $\text{[math]}$ 图象上的点，点Q为其牵引函数图象上的点，求PQ的最小值．
答案解析收藏纠错 + 选题
26. (2023·重庆市模拟) 如图，在△ABC中，AD平分∠BAC交BC于点D ，点E是AB上的一点，连接DE ．
1. （1）如图1，若∠BAC＝90°，∠DEA＝60°，DE＝4，求AE的长度；
2. （2）如图2，过点E作EF平行于AC交BC于点F ，且∠C＝∠BDE+∠AED ，求证：FD＝CD；
3. （3）如图3，在（2）的条件下，过点D作DG⊥BC于点D且交AB于点G ，在BD上取点H使得AH＝EG ，连接AH分别交GD、ED于点M、N ．若∠HAD＝∠B ， ∠HMD＝2∠BDE ，设tan∠AHC $\text{[math]}$ ，请直接写出sin∠BGD的值（用关于a、b的代数式（最简形式）表示）．
答案解析收藏纠错 + 选题