河南省郑州市四禾美术学校2023-2024学年高三上册数学8...

更新时间：2023-12-09 浏览次数：48 类型：月考试卷

一、选择题：本题共12小题，每小题5分，共计60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1. (2023高三上·郑州月考) 设全集U＝{－2，－1，0，1，2，3}，集合A＝{－1，2}，B＝{x∈Z｜x²－4x＋3≤0}，则∁_U（A∪B）＝（）

A . {1，3} B . {0，3} C . {－2，1} D . {－2，0}

答案解析收藏纠错 + 选题
2. (2023高三上·郑州月考) 已知(1－i)²z＝3＋2i，则z＝（）

A . －1－ $\text{[math]}$ i B . －1＋ $\text{[math]}$ i C . － $\text{[math]}$ ＋i D . － $\text{[math]}$ －i

答案解析收藏纠错 + 选题
3. (2023高三上·郑州月考) 下列结果正确的是（）

A . $\text{[math]}$ B . log_a（MN）＝log_aM＋log_aN C . $\text{[math]}$ D . (log₃2＋log₉2)·(log₄3＋log₈3)= $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023高三上·郑州月考) 下列命题正确的是（）

A . 已知x∈R，则“x＜－1”是“x²＞1”的必要不充分条件 B . 已知命题p：∀x≥0，e^x≥1或sinx＜1，则¬p为∃x＜0，e^x＜1且sinx≥1 C . 函数 $\text{[math]}$ 的最小值是4 D . 不等式－2x²＋x＋3＜0的解集为 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023高三上·郑州月考) 某校为了解学生体能素质，随机抽取了100名学生进行体能测试，并将这100名学生成绩整理得如下频率分布直方图.根据此频率分布直方图，下列结论中正确的是（）

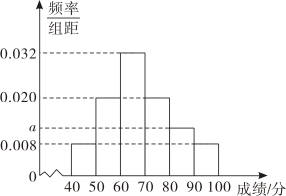
A . 图中a＝0.12 B . 这100名学生中成绩在[50，70）内的人数为50 C . 这100名学生成绩的中位数为70 D . 这100名学生的平均成绩为68.2（同一组中的数据用该组区间的中点值做代表）

答案解析收藏纠错 + 选题
6. (2023高三上·郑州月考) 已知定义在R上的函数f(x)，给出的下列性质中不正确的是（）

A . 对 $\text{[math]}$ ，都有 $\text{[math]}$ 则f(x)是R上的增函数. B . 对 $\text{[math]}$ ，都有f(x)+f(-x)＝0，若f(x)的最大值为M最小值为N，则M+N=0. C . 对 $\text{[math]}$ ，都有f(x)=f(2a-x)(a>0)，则f(x)是R上的周期函数. D . 对 $\text{[math]}$ ，都有f(a+x)=f(a-x)，则f(x)的图象关于直线x=a对称.

答案解析收藏纠错 + 选题
7. (2023高三上·郑州月考) 某人参加一次考试，共有4道试题，至少答对其中3道试题才能合格.若他答每道题的正确率均为0.5，并且答每道题之间相互独立，则他能合格的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023高三上·郑州月考) 已知函数f（x）＝x²－xf'（1），则曲线y＝f（x）在点（2，f（2））处的切线方程为（）

A . 3x－y－4＝0 B . 3x－y＋4＝0 C . 3x＋y＋4＝0 D . 3x＋y－4＝0

答案解析收藏纠错 + 选题
9. (2023高三上·郑州月考) 第24届冬奥会开幕式于2022年2月4日在北京举行.本届冬奥会开幕式上的“大雪花”融合了中国诗词、中国结和剪纸技艺等中国传统文化元素，很好地将奥林匹克精神和中国人民的友谊传递到世界各个角落，获得了世界人民的普遍赞誉.为弘扬中华优秀传统文化，某艺术中心将举办一次以“雪花”为主题的剪纸比赛.要求参赛选手完成规定作品和创意设计作品各2幅，若选手共有不少于3幅作品入选，则该选手将获得“冰雪之韵”纪念品.某选手完成了规定作品和创意设计作品各6幅，指导教师评定其中规定作品4幅和创意设计作品3幅符合入选标准，现从这12幅作品中随机抽取规定作品和创意设计作品各2幅，则指导教师预测该选手获得“冰雪之韵”纪念品的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023高三上·郑州月考) 已知a=log₅0.2 ， b=log₀_.₅0.2 ， c=0.5⁰^.² ，则a，b，c的大小关系为（）

A . a<c<b B . a<b<c C . b<c<a D . c<a<b

答案解析收藏纠错 + 选题
11. (2023高三上·郑州月考) 已知直线 $\text{[math]}$ 经过函数 $\text{[math]}$ 图象过的定点，则 $\text{[math]}$ 的最小值为（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
12. (2023高三上·郑州月考) 已知函数 $\text{[math]}$ 若关于x的方程f(x)+x-a=0有且只有一个实根，则实数a的取值范围是（）

A . (1，+∞) B . [1，+∞） C . （-∞，1] D . (-∞，1）

答案解析收藏纠错 + 选题

二、填空题（本大题共4小题，每小题5分，共20分，把答案填在答题卡上.）

13. (2023高三上·郑州月考) log₃81－log₉8·log₂3－ $\text{[math]}$ ＝.

答案解析收藏纠错 + 选题
14. (2023高三上·郑州月考) $\text{[math]}$ 的展开式中系数为有理数的各项系数之和为.

答案解析收藏纠错 + 选题
15. (2023高三上·郑州月考) 已知函数 $\text{[math]}$ ，若f(x－4)>f(2x－3)，则实数x的取值范围是．

答案解析收藏纠错 + 选题
16. (2023高三上·郑州月考) 已知函数f(x)=2^x-2^-^x ，则当实数t满足f(lnt)-f(1)>0时t的取值范围为.

答案解析收藏纠错 + 选题

三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）

17. (2023高三上·郑州月考) 已知二次函数 $\text{[math]}$ ＝ax²＋bx＋c ，满足 $\text{[math]}$ .
1. （1）求函数 $\text{[math]}$ 的解析式；
2. （2）求 $\text{[math]}$ 在区间 $\text{[math]}$ 上的值域.
答案解析收藏纠错 + 选题
18. (2023高三上·郑州月考) 已知函数 $\text{[math]}$ 且点（4，2）在函数f（x）的图象上.
1. （1）求函数f（x）的解析式，并在图中的直角坐标系中画出函数f（x）的图象；
2. （2）求不等式f（x）＜1的解集.
答案解析收藏纠错 + 选题
19. (2023高三上·郑州月考) 第五代移动通信技术（简称5G）是最新一代蜂窝移动通信技术，是实现人机物互联的网络基础设施.某市工信部门为了解本市5G手机用户对5G网络的满意情况，随机抽取了本市200名5G手机用户进行了调查，所得情况统计如下：
满意
情况
年龄
合计
50岁以下
50岁或50岁以上
满意
95

不满意

25

合计
120

200
1. （1）完成上述列联表，并估计本市5G手机用户对5G网络满意的概率；
2. （2）依据小概率值α＝0.05的独立性检验，分析本市5G手机用户对5G网络满意与年龄在50岁以下是否有关.
  附：
  α
  0.10
  0.05
  0.025
  0.010
  0.001
  x_α
  2.706
  3.841
  5.024
  6.635
  10.828
  $\text{[math]}$ ，其中n＝a＋b＋c＋d.
答案解析收藏纠错 + 选题
20. (2023高三上·郑州月考) 已知函数f(x)=a^x+b，g(x)=log_ax，(a>0，a≠1)，其中a ， b均为实数.
1. （1）若函数f(x)的图像经过点A(0，2)，B(1，3)，求a，b的值；
2. （2）如果函数f(x)的定义域和值域都是[-1，0]，求a+b的值.
3. （3）若a满足不等式2²^a+¹>2⁵^a-² ，且函数g(2x-1)在区间[1，3]上有最小值-2，求实数a的值.
答案解析收藏纠错 + 选题
21. (2023高三上·郑州月考) 为了监控某一条生产线的生产过程，从其产品中随机抽取100件，测量这些产品的质量指标值，由测量结果得到如图所示的频率分布直方图，其中质量指标值落在区间[55，65），[65，75），[75，85]内的频率是公比为 $\text{[math]}$ 的等比数列.
1. （1）求这些产品质量指标值落在区间[75，85]内的频率；
2. （2）若将频率视为概率，从该条生产线的这种产品中随机抽取3件，记这3件产品中质量指标值位于区间[45，75）内的产品件数为X ，求X的分布列与数学期望.
答案解析收藏纠错 + 选题
22. (2023高三上·郑州月考) 已知函数 $\text{[math]}$ (x∈R，e为自然对数的底数).
1. （1）求 $\text{[math]}$ 的单调区间；
2. （2）求函数 $\text{[math]}$ 在区间[0，m]上的最大值和最小值.
答案解析收藏纠错 + 选题