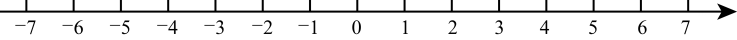一、选择题(本大题共6小题,每小题3分,共18分)
-
-
-
A . 正有理数和负有理数统称为有理数;
B . 绝对值等于本身的数是正数;
C . 有理数不是整数就是分数;
D . 0是最小的整数
-
-
A . 相等
B . 互为相反数
C . 都是0
D . 互为相反数或相等
-
二、填空题(本大题共6小题,每小题3分,共18分)
-
-
-
-
10.
(2023七上·吉安月考)
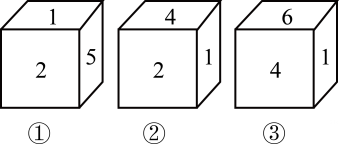
已知一个不透明的正方体的六个面上分别写着1至6六个数字,如图是我们能看到的三种情况,那么4所在面的对面是
.
-
11.
(2023七上·吉安月考)
已知一个直角三角形的两条直角边的长分别是3cm,4cm.将这个直角三角形绕它的较长的直角边所在的直线旋转一周,可以得到一个圆锥,则这个圆锥的体积是
.(结果保留π).
-
三、解答题(本大题共5小题,每小题6分,共30分)
-
-
(1)
计算:

-
(2)
计算:

.
-
-
(1)
在数轴上画出表示各数的点;

-
-
15.
(2023七上·吉安月考)
将下列各数填在相应的集合内:2.1,0,

,

,

,

.
整数集合:{ }…
分数集合:{ }…
非负数合:{ }…
-
-
-
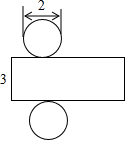
(2)
根据图中所给信息,求该几何体的侧面积和体积(结果保留

)
-
四、解答题(本大题共3小题,每小题8分,共24分)
-
-
(1)
将最后一名志愿者送到目的地时,小王在哪个位置?
-
(2)
若每千米耗油0.5L,则小王一上午耗油多少升?
-
-
(1)
请画出从正面、左面和上面看到的这个几何体的形状图;
-
(2)
若每个小立方块的棱长为1,请计算它的表面积.
-
20.
(2023七上·沙坪坝期中)
把几个数用大括号括起来,中间用逗号断开,如:

,

, 我们称之为集合,其中的数称为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数

也必是这个集合的元素,这样的集合我们称为“好”的集合.例如,集合

就是一个“好”的集合.
-
(1)
请你判断集合

,

是不是“好”的集合;
-
(2)
请你再写出一个“好”的集合(不得与由上面出现过的集合重复);
-
(3)
写出所有“好”的集合中,元素个数最少的集合.
五、解答题(本大题共2小题,每小题9分,共18分)
-
21.
(2023七上·吉安月考)
科技改变生活,当前网络销售日益盛行,许多农商采用网上销售的方式进行营销,实现脱贫致富。小明把自家种的柚子放到网上销售,计划每天销售100千克,但实际每天的销售量与计划销售量相比有增减,超过计划量记为正,不足计划量记为负。下表是小明第一周柚子的销售情况:(单位:千克)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
柚子销售计划量情况 | +3 |  |  | +11 |  | +13 | +5 |
-
(1)
小明第一周销售柚子最多的一天比最少的一天多销售多少千克?
-
-
(3)
若小明按8元/千克进行柚子销售,平均运费为3元/千克,则小明第一周销售柚子一共收入多少元?
-
-
(1)

;
-
(2)
计算:

;
-
(3)
拓展,计算:

.
-
-
(1)
数轴上表示4和1的两点之间的距离
▲ ;表示

和2两点之间的距离是
▲ ;一般地数轴上表示数m和数n的两点之间的距离等于

.如果表示数a和

的两点之间的距离是3,求a的值.
-
(2)
若数轴上表示数a的点位于

与2之间,求

的值.
-
(3)
利用数轴找出所有符合条件的整数点x,使得

, 求这些点表示的数的和.
-
(4)
当a=
时,

的值最小,最小值是
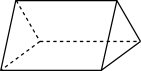 B .
B . 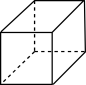 C .
C . 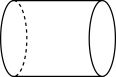 D .
D . 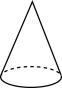
![]()
![]()

![]()
,
, +6,
,
,
, +4,+6,
,