浙江省绍兴市诸暨暨阳初中教育共同体2023学年八年级第一学期...

更新时间：2024-02-27 浏览次数：50 类型：月考试卷

一、选择题（本大题共10小题，每小题3分，共30分，每小题有且只有一个正确答案）

1. (2024八上·鄱阳期中) 已知三角形的两边长分别为4cm和8cm ，则第三边的长可以是（）

A . 4cm B . 8cm C . 12cm D . 16cm

答案解析收藏纠错 + 选题
2. (2023八上·诸暨月考) 下列每组中的两个图形，是全等形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024八上·沅江开学考) 下列命题中，属于假命题的是（）

A . 等底等高的两个三角形的面积相等 B . 三角形的外角和等于内角和的2倍 C . 三角形的一个外角等于两个内角的和 D . 全等三角形的面积相等

答案解析收藏纠错 + 选题
4. (2023八上·诸暨月考) 下列说法中，正确的是（）

A . 三角形的三条高都在三角形内 B . 三角形的一个外角大于任何一个内角 C . 三角形的一条中线把三角形分成面积相等的两个三角形 D . 三角形中，到三边距离相等的点是这个三角形三条边的垂直平分线的交点

答案解析收藏纠错 + 选题
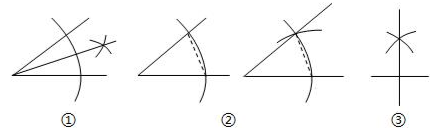
5. (2023八上·诸暨月考) 下列尺规作图分别表示：①作一个角的平分线；②作一个角等于已知角；③作一条线段的垂直平分线.其中作法正确的是（）

A . ①② B . ①③ C . ②③ D . ①②③

答案解析收藏纠错 + 选题
6. (2023八上·诸暨月考) 如图，点B ， E ， C ， F共线，∠B＝∠DEF ， BE＝CF ，添加一个条件，不能判断△ABC≌△DEF的是（）

A . AB＝DE B . ∠A＝∠D C . AC＝DF D . AC∥DF

答案解析收藏纠错 + 选题
7. (2023八上·诸暨月考) 如图，将两根钢条 $\text{[math]}$ 、 $\text{[math]}$ 的中点 $\text{[math]}$ 连在一起，使 $\text{[math]}$ 、 $\text{[math]}$ 可以绕着点 $\text{[math]}$ 自由转动，就做成了一个测量工件，由三角形全等得出 $\text{[math]}$ 的长等于内槽宽 $\text{[math]}$ ；那么判定 $\text{[math]}$ 的理由是（）

A . 边角边 B . 角边角 C . 边边边 D . 角角边

答案解析收藏纠错 + 选题
8. (2023八上·诸暨月考) 如图， $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 边中线，若 $\text{[math]}$ 的周长为8，则 $\text{[math]}$ 的周长是（）

A . 8 B . 9 C . 10 D . 12

答案解析收藏纠错 + 选题
9. (2023八上·诸暨月考) 如图，在 $\text{[math]}$ 中，点D在AC上，BD平分 $\text{[math]}$ ，延长BA到点E ，使得 $\text{[math]}$ ，连接DE ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . 68° B . 69° C . 71° D . 72°

答案解析收藏纠错 + 选题
10. (2023八上·诸暨月考) 如图，AD是△ABC的中线，点E ， F分别在AB ， AC上（点E ， F不与端点重合）且DE⊥DF.则线段BE ， CF ， EF的关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 与EF的大小关系不确定

答案解析收藏纠错 + 选题

二、填空题（本大题共10小题，每小题3分，共30分.请把答案填在题中的横行上）

11. (2023八上·诸暨月考) 命题“两直线平行，同位角相等”的条件是，结论是．

答案解析收藏纠错 + 选题
12. (2023八上·诸暨月考) 如图所示，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，外角 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2023八上·诸暨月考) 如图，AC＝AD ， ∠1＝∠2，要使△ABC≌△AED ，应添加的条件是．(写一个）

答案解析收藏纠错 + 选题
14. (2023八上·诸暨月考) 如图，将△ABC沿BC所在的直线平移得到△A′B′C′，则∠C′的对应角为，AC的对应边为．

答案解析收藏纠错 + 选题
15. (2023八上·诸暨月考) 设a、b、c是△ABC的三边，化简：|a+b﹣c|﹣|b﹣c﹣a|＝．

答案解析收藏纠错 + 选题
16. (2024八上·杭州期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 的垂直平分线.若 $\text{[math]}$ ， $\text{[math]}$ 的周长为13，则 $\text{[math]}$ 的周长为.

答案解析收藏纠错 + 选题
17. (2023八上·诸暨月考) 如图，①在OA、OB上分别截取线段OD、OE ，使OD=OE；②分别以 $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径画弧，在 $\text{[math]}$ 内两弧交于点 $\text{[math]}$ ；③作射线 $\text{[math]}$ ．若∠AOB=60° ，则 $\text{[math]}$ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2023八上·诸暨月考) 如图，△ABC中， $\text{[math]}$ 是 $\text{[math]}$ 边上的中线， $\text{[math]}$ 是 $\text{[math]}$ 中 $\text{[math]}$ 边上的中线，若 $\text{[math]}$ 的面积是28，则 $\text{[math]}$ 的面积．

答案解析收藏纠错 + 选题
19. (2023八上·诸暨月考) 如图，在△ABC中，∠B＝∠C＝65°，BD＝CE ， BE＝CF ，则∠DEF的度数是．

答案解析收藏纠错 + 选题
20. (2023八上·诸暨月考) 如图，在Rt△ABC中，∠ACB=90°，△ABC的角平分线AD ， BE相交于点P ，过P作PF⊥AD ，交BC延长线于F ，交AC于H ，则下列结论：①∠APB=135°；②BF=BA；③ $\text{[math]}$ =HC；④PH=PD；其中正确的有．

答案解析收藏纠错 + 选题

三、解答题（本大题共5小题，共40分，写出必要的文字说明，证明过程或演算步骤）

21. (2023八上·诸暨月考) 已知：线段a ， ∠α ， ∠β ．
尺规作图求作：△ABC ，使BC＝a ， ∠B＝∠α ， ∠C＝∠β ．（保留作图痕迹）

答案解析收藏纠错 + 选题
22. (2023八上·诸暨月考) 如图，∠ABD＝∠CBE ， BA＝BD ， BC＝BE ，点C恰好落在DE边上．
1. （1）求证：△ABC≌△DBE；
2. （2）若∠ABD=30°，求∠ACD的度数．
答案解析收藏纠错 + 选题
23. (2023八上·诸暨月考) 如图，在△ABC中，AD是高，AE ， BF是角平分线，它们相交于点O ．
1. （1）若∠ABC＝60°，∠C＝70°，求∠DAE的度数．
2. （2）若∠ABC＝α ， ∠C＝β（α＜β），则∠DAE＝．（用含α、β的式子表示）
答案解析收藏纠错 + 选题
24. (2023八上·诸暨月考) 如图，在△ABC中，AB=CB ， ∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD ，连结AE ， DE ， CD ．
1. （1）求证：AE=CD ．
2. （2）判断直线AE与CD的位置关系，并说明理由.
答案解析收藏纠错 + 选题
25. (2023八上·诸暨月考) 如图1，已知∠MON=60° ， A、B两点同时从点O出发，点A沿射线ON运动，点B沿射线OM运动．，点C为△ABO三条内角平分线交点，连接BC、AC ．
1. （1）如图2，当∠OAB=70° ，求∠ACB的大小。
2. （2）在点A、B的运动过程中，∠ACB的度数是否发生变化？若不发生变化，求其值；若发生变化，请说明理由：
3. （3）如图3，连接OC并延长，与∠ABM的角平分线交于点P ，与AB交于点Q ．在△BCP中，如果有一个角是另一个角的2倍，直接写出∠BAO的度数．
答案解析收藏纠错 + 选题