一、选择题：本大题共10个小题，每小题3分，共30分．
-
-
A . 圆锥
B . 圆柱
C . 四棱柱
D . 四棱锥
-
-
4.
(2023七上·顺德期中)
中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数．如果收入100元记作+100元。那么一80元表示（ ）
A . 支出20元
B . 收入20元
C . 支出80元
D . 收入80元
-
5.
(2023七上·顺德期中)
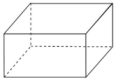
数学课上，小明用白萝卜做了一个如图所示的四棱柱模型．若用一个平面去截该模型，截面的形状不可能是（ ）
-
A . 
B . 0
C . 1
D . 2
-
7.
(2023七上·顺德期中)
下列说法：①有理数中，0的意义仅表示没有；②任何有理数都有倒数；③正数和负数统称有理数；④两数相加，和一定大于其中一个加数．其中正确的个数（ ）
A . 0个
B . 1个
C . 2个
D . 3个
-
A . 这个棱柱是十二棱柱
B . 这个棱柱有4个侧面
C . 这个棱柱的底面是八边形
D . 这个棱柱有6条侧棱
-
-
10.
(2023七上·顺德期中)
如图，将一个边长为1的正方形纸片分割成7个部分，部分①是整体面积的一半，部分②是部分①面积的一半，依次类推，则
的值是（ ）
二、填空题：本大题共5小题，每小题3分，共15分．
三、解答题（一）：本大题共3小题，第16题12分，第17、18题各6分，共24分．
-
-
（1）
计算：
．
-
（2）
计算：
．
-
（3）
计算：
．
-
-
（1）
该商品现在的售价为元（用含a的代数式表示）；
-
（2）
若
， 求商品现在的售价．
-
18.
(2023七上·顺德期中)
观察下面由6个相同的小立方块组成的几何体，请在指定的位置画出从这个几何体的正面，左面、上面看到的形状图．
四、解答题（二）：本大题共3小题，每小题9分，共27分．
-
19.
(2023七上·顺德期中)
某牛奶厂从生产的盒装牛奶中抽出样品20盒，检测每盒的容量是否符合标准，超过的部分用正数表示，不足的部分用负数表示，记录如表：
与标准容量的差值（mL） | -4 | -2 | 0 | 1 | 3 | 5 |
盒数（盒） | 2 | 3 | 6 | 4 | 4 | 1 |
-
（1）
若每盒标准容量为250mL，则这批样品的总容量是多少mL？
-
（2）
若该牛奶的盒子上标有产品合格要求为“净含重
”，则这批样品的合格率为多少？
-
20.
(2023七上·顺德期中)
综合与实践
【问题情境】如图，现有一张边长为20cm的正方形废弃宣传单，小华准备将其四个角各剪去一个小正方形，折成无盖长方体形纸盒．
-
（1）
【操作探究】剪去的小正方形的边长按整数值依次变化，即分别取1cm，2cm，3cm，4cm，5cm，6cm，7cm，8cm，9cm，10cm时，折成的无盖长方体的容积分别是多少？请你将计算的结果填入下表；
剪去正方形的边长/cm | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
容积 | 324 | 512 |
|
| 500 | 384 | 252 | 128 | 36 | 0 |
-
（2）
【操作分析】观察绘制的统计表，你发现，随着减去的小正方形的边长的增大，所折无盖长方体盒子的容积如何变化？____
A . 一直增大
B . 一直减小
C . 先增大后减小
D . 先减小后增大
-
（3）
分析猜想当剪去图形的边长为
cm时，所得的无盖长方体的容积最大，此时无盖长方体的容积是
．
-
（4）
【操作反思】对（1）中的结果，你觉得表格中的数据还有什么要改进的地方吗？
-
21.
(2023七上·顺德期中)
小华在学习了整式一章中的字母表示数的内容后，对用字母表示规律产生了浓厚的兴趣，他用完全相等的小木棒搭建了如图所示的四个图形．
图1 图2 图3 图4
-
（1）
观察图形，其中图1用了根小木棒，图2用了根小木棒，图3用了根小木棒；
-
（2）
若按小华的方式继续搭建，猜想第n个图形中，小木棒的根数是多少？
-
（3）
根据（2）中的猜想，当
时，用了多少根小木棒？
五、解答题（三）：本大题共2小题，每小题12分，共24分．
-
22.
(2023七上·顺德期中)
综合探究
2023年“十一黄金周”假期，恰逢中秋国庆双节，文化和旅游行业的消费恢复势头强劲．某风景区在黄金周8天假期内，每天旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）．
日期 | 9月29日 | 9月30日 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 |
变化/万人 | 1.2 | -0.2 | 0.8 | -0.4 | 0.6 | 0.2 | a | -1.2 |
-
（1）
9月29日至10月3日这五天中，到该风景区的旅客人数最多的是哪一天？最少的是哪一天？它们相差多少万人？（直接写出答案）
-
（2）
若9月28日的旅客人数为2万人，10月6日到该风景区的旅客人数与9月28日的旅客人数持平．
①
；
②此风景区一方面给广大市民提供一个休闲游玩的好去处；另一方面拉动了内需，促进了消费．若在此风景区每人平均消费200元，请求出“十一黄金周”8天假期所有游客的总消费是多少万元？
-
-
（1）
数轴上表示2和7的两点之间的距离的值是
；数轴上表示
x与
的两点之间的距离可记作
，如果这两点之间的距离为3，那么
；
-
（2）
利用数轴，找出所有符合条件的整数
x ， 使
；
-
（3）
若
x表示有理数，直接写出：
的最小值．
B . 
C . 
D . 
