一、选择题(本大题共10小题, 每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
A .  B . 0
C . 1
D . 2
B . 0
C . 1
D . 2
-
-
3.
(2023九上·南海期中)
参加夏季篮球联赛的每两支球队之间都要进行一场比赛,共要比赛28场.设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )
-
4.
(2023九上·南海期中)
某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
-
A . 有两个不相等的实数根
B . 没有实数根
C . 有两个相等的实数
D . 无法确定
-
6.
(2023九上·南海期中)
在一个不透明的空袋子里,放入仅颜色不同的2个红球和1个白球,从中随机摸出1个球后不放回,再从中随机摸出1个球,两次都摸到红球的概率是( )
-
7.
(2023九上·南海期中)
在一个不透明的盒子里装着除颜色外完全相同的黑,白两种小球共40个.小颖做摸球试验,她将盆子里面的球搅匀后从中随机摸出一个球记下颜色后放回,不断重复上述过程,多次试验后,得到表中的数据,并得出了以下四个结论,则其中正确的结论是( )
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 70 | 128 | 171 | 302 | 481 | 599 | 1806 |
摸到白球的频率 | 0.75 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
A . 这个盒子中的白球一定有28个
B . 从该盒子中任意摸出一个小球,摸到白球的概率为0.6
C . 试验1500次摸到白球的频率比试验800次的更接近0.6
D . 当试验次数n为2000时,摸到白球的次数m一定等于1200
-
-
9.
(2023九上·南海期中)
▱ABCD中,AC,BD是两条对角线,如果添如一个条件,可推出▱ABCD是菱形,那么这个条件可以是( )

A . AB=CD
B . AC=BD
C . AC⊥BD
D . AB⊥BD
-
10.
(2023九上·南海期中)
如图,两张等宽的纸条交叉叠放在一起,重合部分构成四边形

.测得A,B的距离为3,A,C的距离为2,则B,D的距离是( )

二、填空题:本大题共5小题,每小题3分,共15分.
-
-
-
-
-
15.
(2023九上·南海期中)
一块矩形绸布的宽

, 长

, 按照图中所示的方式将它裁成相同的n面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,那么a的值应当是
.
三、解答题(一):本大题共3小题,第16题10分,第17.18题各7分,共24分.
-
-
(1)
解方程:

;
-
(2)
若a是关于x的一元二次方程

的根,求代数式

的值.
-
17.
(2023九上·南海期中)
中国古代有着辉煌的数学成就,A《周髀算经》,B《九章算术》,C《海岛算经》,D《孙子算经》等是我国古代数学的重要文献.
-
(1)
小聪想从这4部数学名著中随机选择1部阅读,则他选中B《九章算术》的概率为;
-
(2)
某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容,求恰好选中B《九章算术》和D《孙子算经》的概率.
-
-
(1)
求证:不论k取任何实数值,方程总有实数根;
-
(2)
若

斜边长

, 另两边长b,c恰好是这个方程的两个根,求

的周长.
四、解答题(二):本大题共3小题,每小题9分,共27分.
-
19.
(2023九上·南海期中)
阅读材料:若

, 求m、n的值.
解:∵ , ∴
, ∴ .
.
∴ , ∴
, ∴ ,
,  , ∴
, ∴ ,
,  .
.
根据你的观察,探究下面的问题:
-
(1)
已知

, 求

的值.
-
(2)
已知

的三边长a、b、c都是正整数,且满足

, 求边c的值.
-
20.
(2023九上·南海期中)
某商场今年初以每件40元的进价购进一品商品,当商品销售价为60元时,一月份销售64件,二、三月份该商品十分畅销,销售量持续走高.在售价不变的基础上,三月底的销售量达到100作,设二、三月份这两个平均增长率不变.
-
-
(2)
从四月起,商场决定采用降价促销,经调查发现,该商品每降价2元,销售量增加20件,为尽可能让利于顾客,赢得市场,该商品每件应降价多少元出售,使商场月获利2240元?
-
-
(1)
求证:四边形

是菱形;
-
(2)
当

满足什么条件时,四边形

是正方形?请说明理由.
五、解答题(三):本大题共2小题,每小题12分,共24分.
-
22.
(2023九上·南海期中)
如图,在矩形

中,

,

.点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为

, 点F的速度为

, 当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第1秒时,

的面积为

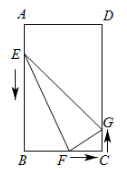
-
(1)
当

秒时,S的值是多少?
-
(2)
写出S和t之间的函数关系式,并指出自变量t的取值范围;
-
(3)
若点F在矩形的边

上移动,当t为何值时,以点E、B、F为顶点的三角形与以点F、C、G为顶点的三角形相似?请说明理由.
-
-
-
(2)
在直线

上有一个动点M,过M点作直线

轴,与直线

相交于点N,若

的面积为6,求M点的坐标.
-
(3)
若点C为线段

上一动点,在平面内是否存在点D,使得以点O,A,C,D为顶点的四边形是菱形,若存在请直接写出D点的坐标,若不存在请说明理由.

中,
, D、E两点分别为
、
两边的平行线,与
的延长线相交于点F,连接
、
.

