四川省成都市青羊区2023-2024学年高二上学期数学期中试...

更新时间：2024-01-16 浏览次数：28 类型：期中考试

一、单选题：本题共8小题，每小题5分，共40分.在每个小题给出的四个选项中，只有一项是符合题目要求的.

1. (2023高二上·青羊期中) 空间向量 $\text{[math]}$ ，若 $\text{[math]}$ ，则实数 $\text{[math]}$ （）

A . 1 B . -2 C . 0 D . 2

答案解析收藏纠错 + 选题
2. (2023高二上·青羊期中) 已知直线的方程为 $\text{[math]}$ ，则该直线的倾斜角 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023高二上·青羊期中) 已知圆 $\text{[math]}$ 的方程为 $\text{[math]}$ ，圆 $\text{[math]}$ 的方程为 $\text{[math]}$ ，若圆 $\text{[math]}$ 与圆 $\text{[math]}$ 外切，则 $\text{[math]}$ 的值为（）

A . 1 B . 9 C . 10 D . 16

答案解析收藏纠错 + 选题
4. (2023高二上·青羊期中) 在斜三棱柱 $\text{[math]}$ 的底面 $\text{[math]}$ 中， $\text{[math]}$ ，且 $\text{[math]}$ ，则线段 $\text{[math]}$ 的长度是（）

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
5. (2023高二上·青羊期中) 在棱长为2的正方体 $\text{[math]}$ 中， $\text{[math]}$ 分别是棱 $\text{[math]}$ 上的动点，且 $\text{[math]}$ ，当三棱锥 $\text{[math]}$ 的体积最大时，直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正弦值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023高二上·青羊期中) 已知圆 $\text{[math]}$ ，圆 $\text{[math]}$ 分别是圆 $\text{[math]}$ 的动点， $\text{[math]}$ 为直线 $\text{[math]}$ 上的动点，则 $\text{[math]}$ 的最小值为（）

A . 6 B . 10 C . 13 D . 16

答案解析收藏纠错 + 选题
7. (2023高二上·青羊期中) 在Rt $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 的中点.将 $\text{[math]}$ 沿 $\text{[math]}$ 进行旋转，得到三棱锥 $\text{[math]}$ ，当二面角 $\text{[math]}$ 为 $\text{[math]}$ 时， $\text{[math]}$ 的外接球的表面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
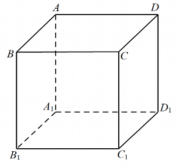
8. (2023高二上·青羊期中) 已知正方体 $\text{[math]}$ 的边长为1，点 $\text{[math]}$ 关于平面 $\text{[math]}$ 对称的点为 $\text{[math]}$ ，矩形 $\text{[math]}$ 内（包括边界）的点 $\text{[math]}$ 满足 $\text{[math]}$ ，记直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成线面角为 $\text{[math]}$ .当 $\text{[math]}$ 最大时，过直线 $\text{[math]}$ 做平面 $\text{[math]}$ 平行于直线 $\text{[math]}$ ，则此时平面 $\text{[math]}$ 截正方体所形成图形的周长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分.

9. (2023高二上·青羊期中) 下列选项正确的是（）

A . 若两条不重合的直线的倾斜角相等，则这两条直线一定平行 B . 若直线 $\text{[math]}$ 与直线 $\text{[math]}$ 垂直，则 $\text{[math]}$ C . 若直线 $\text{[math]}$ 与直线 $\text{[math]}$ 平行，则 $\text{[math]}$ D . 若直线 $\text{[math]}$ 的一个方向向量是 $\text{[math]}$ ，则直线 $\text{[math]}$ 的倾斜角是 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023高二上·青羊期中) 如图，在四棱锥 $\text{[math]}$ 中， $\text{[math]}$ 是矩形，侧棱 $\text{[math]}$ 底面 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ 分别为 $\text{[math]}$ 的中点， $\text{[math]}$ 为线段 $\text{[math]}$ 上的动点，则（）

A . 四面体 $\text{[math]}$ 每个面都是直角三角形 B . $\text{[math]}$ C . 当点 $\text{[math]}$ 异于 $\text{[math]}$ 点时， $\text{[math]}$ $\text{[math]}$ 平面 $\text{[math]}$ D . 直线 $\text{[math]}$ 和平面 $\text{[math]}$ 所成角的正切值为 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高二上·白城期中) 点 $\text{[math]}$ 是圆 $\text{[math]}$ 上的动点，则下面正确的有（）

A . 圆的半径为3 B . $\text{[math]}$ 既没有最大值，也没有最小值 C . $\text{[math]}$ 的范围是 $\text{[math]}$ D . $\text{[math]}$ 的最大值为72

答案解析收藏纠错 + 选题
12. (2023高二上·青羊期中) 已知圆 $\text{[math]}$ ，点 $\text{[math]}$ .过点 $\text{[math]}$ 作圆 $\text{[math]}$ 的两条切线 $\text{[math]}$ 为切点，则下列说法正确的有（）

A . 当 $\text{[math]}$ 时，不存在实数 $\text{[math]}$ ，使得线段 $\text{[math]}$ 的长度为整数 B . 若 $\text{[math]}$ 是圆 $\text{[math]}$ 上任意一点，则 $\text{[math]}$ 的最小值为 $\text{[math]}$ C . 当 $\text{[math]}$ 时，不存在点 $\text{[math]}$ ，使得 $\text{[math]}$ 的面积为1 D . 当 $\text{[math]}$ 且 $\text{[math]}$ 时，若在圆 $\text{[math]}$ 上总是存在点 $\text{[math]}$ ，使得 $\text{[math]}$ ，则此时 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分，共20分.

13. (2023高二上·青羊期中) 已知直线 $\text{[math]}$ 与圆 $\text{[math]}$ ，则直线 $\text{[math]}$ 被圆 $\text{[math]}$ 所截得的弦长为.

答案解析收藏纠错 + 选题
14. (2023高二上·青羊期中) 在三棱锥 $\text{[math]}$ 中， $\text{[math]}$ 在线段 $\text{[math]}$ 上，满足 $\text{[math]}$ 是平面 $\text{[math]}$ 内任意一点， $\text{[math]}$ ，则实数 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2023高二上·青羊期中) 在空间直角坐标系中，若一条直线经过点 $\text{[math]}$ ，且以向量 $\text{[math]}$ 为方向向量，则这条直线可以用方程 $\text{[math]}$ 来表示，已知直线 $\text{[math]}$ 的方程为 $\text{[math]}$ ，则点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离为.

答案解析收藏纠错 + 选题
16. (2023高二上·青羊期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，过 $\text{[math]}$ 中点 $\text{[math]}$ 的动直线 $\text{[math]}$ 与线段 $\text{[math]}$ 交于点 $\text{[math]}$ ，将 $\text{[math]}$ 沿直线 $\text{[math]}$ 向上翻折至 $\text{[math]}$ ，使得点 $\text{[math]}$ 在平面 $\text{[math]}$ 内的射影 $\text{[math]}$ 落在线段 $\text{[math]}$ 上，则斜线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正弦值的取值范围为.

答案解析收藏纠错 + 选题

四、解答题：本题共6小题，第17小题10分，其余小题每题12分，共70分.解答题应写出文字说明､证明过程或演算步骤.

17. (2023高二上·青羊期中) 已知点 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的坐标；
2. （2）求以 $\text{[math]}$ 为邻边的平行四边形的面积.
答案解析收藏纠错 + 选题
18. (2023高二上·青羊期中) 已知直线 $\text{[math]}$ 经过 $\text{[math]}$ 两点， $\text{[math]}$ .
1. （1）求直线 $\text{[math]}$ 和直线 $\text{[math]}$ 的一般式方程；
2. （2）已知直线 $\text{[math]}$ 经过直线 $\text{[math]}$ 与直线 $\text{[math]}$ 的交点，且在 $\text{[math]}$ 轴上的截距是在 $\text{[math]}$ 轴上的截距的4倍，求直线 $\text{[math]}$ 的一般式方程.
答案解析收藏纠错 + 选题
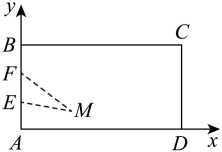
19. (2023高二上·青羊期中) 如图所示，有一个矩形坐标场地 $\text{[math]}$ （包含边界和内部， $\text{[math]}$ 为坐标原点）， $\text{[math]}$ 长为8米，在 $\text{[math]}$ 边上距离 $\text{[math]}$ 点4米的 $\text{[math]}$ 处放置一个行走仪，在距离 $\text{[math]}$ 点2米的 $\text{[math]}$ 处放置一个机器人，机器人行走速度为 $\text{[math]}$ ，行走仪行走速度为 $\text{[math]}$ ，若行走仪和机器人在场地内沿直线方向同时到达场地内某点 $\text{[math]}$ ，那么行走仪将被机器人捕获，称点 $\text{[math]}$ 叫捕获点.
1. （1）求在这个矩形场地内捕获点 $\text{[math]}$ 的轨迹方程；
2. （2）若 $\text{[math]}$ 为矩形场地 $\text{[math]}$ 边上的一点，若行走仪在线段 $\text{[math]}$ 上都能逃脱，问： $\text{[math]}$ 点的位置应在何处？
答案解析收藏纠错 + 选题
20. (2023高二上·青羊期中) 如图，在四棱锥 $\text{[math]}$ 中， $\text{[math]}$ 是边长为3的正三角形， $\text{[math]}$ ，平面 $\text{[math]}$ 平面 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求二面角 $\text{[math]}$ 的平面角的正切值.
答案解析收藏纠错 + 选题
21. (2023高二上·青羊期中) 如图，菱形 $\text{[math]}$ 的边长为 $\text{[math]}$ 为 $\text{[math]}$ 的中点.将 $\text{[math]}$ 沿 $\text{[math]}$ 折起，使 $\text{[math]}$ 到达 $\text{[math]}$ ，连接 $\text{[math]}$ ，得到四棱锥 $\text{[math]}$ .
1. （1）证明： $\text{[math]}$ ；
2. （2）当二面角 $\text{[math]}$ 的平面角在 $\text{[math]}$ 内变化时，求直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正弦值的最大值.
答案解析收藏纠错 + 选题
22. (2023高二上·青羊期中) 已知圆 $\text{[math]}$ 和点 $\text{[math]}$ .
1. （1）过点 $\text{[math]}$ 向圆 $\text{[math]}$ 引切线，求切线的方程.
2. （2）点 $\text{[math]}$ 是圆 $\text{[math]}$ 上任意一点， $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上，且点 $\text{[math]}$ 是线段 $\text{[math]}$ 的中点，求 $\text{[math]}$ 点运动的轨迹 $\text{[math]}$ 的方程.
3. （3）设圆 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ 两点，线段 $\text{[math]}$ 上的点 $\text{[math]}$ 上满足 $\text{[math]}$ ，若 $\text{[math]}$ 直线 $\text{[math]}$ ，且直线 $\text{[math]}$ 与（2）中曲线 $\text{[math]}$ 交于 $\text{[math]}$ 两点，满足 $\text{[math]}$ .试探究是否存在这样的直线 $\text{[math]}$ ，若存在，请说明理由并写出直线 $\text{[math]}$ 的斜率，若不存在，请说明理由.
答案解析收藏纠错 + 选题