浙江省湖州市安吉县2023-2024学年八年级第一学期数学期...

更新时间：2024-01-28 浏览次数：54 类型：期中考试

一、仔细选一选（本题有10个小题，每小题3分，共30分）

1. (2023八上·安吉期中) 下列四组线段中，能组成三角形的是（）

A . 2cm，3 cm，4 cm B . 3 cm，4 cm，7 cm C . 4 cm，6 cm，2 cm D . 7 cm，10 cm，2 cm

答案解析收藏纠错 + 选题
2. (2024八上·凉州期末) 如图，下列图案是我国几家银行的标志，其中不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023八上·安吉期中) 若x＞y，则下列式子中错误的是（）

A . x－3＞y－3 B . $\text{[math]}$ ＞ $\text{[math]}$ C . x＋3＞y＋3 D . －3x＞－3y

答案解析收藏纠错 + 选题
4. (2023八上·安吉期中) 下列对△ABC的判断，错误的是（）

A . 若∠A：∠B：∠C＝1：2：3，则△ABC是直角三角形 B . 若∠A＝30°，∠B＝50°，则△ABC是锐角三角形 C . 若AB＝AC，∠B＝40°，则△ABC是钝角三角形 D . 若2∠A＝2∠B＝∠C，则△ABC是等腰直角三角形

答案解析收藏纠错 + 选题
5. (2023八上·安吉期中) 在数轴上表示不等式x≥-2的解集，正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2023八上·安吉期中) 如图，尺规作图，作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA，OB于C，D，再分别以点C，D为圆心，以大于 $\text{[math]}$ CD长为半径画弧，两弧交于点P，作射线OP，由作法得△OCP≌△ODP的根据是（）

A . SAS B . ASA C . AAS D . SSS

答案解析收藏纠错 + 选题
7. (2023八上·安吉期中) 如图，在四边形ABCD中，∠DAB＝∠BCD＝90°，分别以四边形ABCD的四条边为边向外作四个正方形，面积分别为S₁ ， S₂ ， S₃ ， S₄ ．若S₁＝48，S₂+S₃＝135，则S₄＝（）

A . 183 B . 87 C . 119 D . 81

答案解析收藏纠错 + 选题
8. (2023八上·安吉期中) 直角三角形的两条边长分别是5和12，则斜边上的中线长是（）

A . 6.5 B . 6 C . 6或2.5 D . 6或6.5

答案解析收藏纠错 + 选题
9. (2023八上·安吉期中) 如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线一点，当PA=CQ时，连结PQ交AC于，则DE的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023八上·安吉期中) 如图是一张长方形纸片ABCD，点M是对角线AC的中点，点E在BC边上，把△DCE沿直线DE折叠，使点C落在对角线AC上的点F处，连接DF、EF，若MF=CD，则∠DAF的度数为（）

A . 15° B . 16° C . 18° D . 20°

答案解析收藏纠错 + 选题

二、认真填一填（本题有6个小题，每小题4分，共24分）

11. (2023八上·安吉期中) 命题：“两直线平行，则同旁内角互补”的逆命题为.

答案解析收藏纠错 + 选题
12. (2023八上·安吉期中) 关于x的不等式2x+a≤0的解集如图所示，则a的值是.

答案解析收藏纠错 + 选题
13. (2023八上·安吉期中)
如图，AE⊥AB，且AE=AB，BC⊥CD，且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是

答案解析收藏纠错 + 选题
14. (2023八上·安吉期中) 如图，△ABC中，AB=AC，点D在AC上，点E在AB上，且AD=DE=EB，BD=BC，那么∠A=．

答案解析收藏纠错 + 选题
15. (2023八上·安吉期中) 如图，Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，AC=3、AB=5，则BD=．

答案解析收藏纠错 + 选题
16. (2023八上·安吉期中) 如图，等腰Rt△ABC的直角边长为 $\text{[math]}$ ， D，E分别为边AB，AC上两个动点，且AE=BD，则CD+BE的最小值.

答案解析收藏纠错 + 选题

三、解答题（本题有8个小题，第17-19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分，解答需写出必要文字说明、验算步骤或证明过程）

17. (2023八上·安吉期中) 在如图所示的正方形网格中，已有两个正方形涂黑，请再将其中的一个空白正方形涂黑，使整个图形是一个轴对称图形最少三种不同方法.

答案解析收藏纠错 + 选题
18. (2023八上·安吉期中) 如图，AB⊥BC，AD⊥DC，AB＝AD，求证：∠1＝∠2．

答案解析收藏纠错 + 选题
19. (2023八上·安吉期中) 如图，在△ABC中，AD，AE分别是边BC上的中线和高．
1. （1）若AE=5cm，面积S_△_ABC=30cm² ，求DC的长；
2. （2）若∠B=40°，∠C=50°，求∠DAE的大小．
答案解析收藏纠错 + 选题
20. (2023八上·安吉期中) 如图，△ABC中，AB=AC，AD⊥BC垂足为点D，CE⊥AB垂足为点E，AE=CE．求证：
1. （1） △AEF≌△CEB；
2. （2） AF=2CD．
答案解析收藏纠错 + 选题
21. (2023八上·安吉期中) 若a、b是△ABC的两边且|a-3|+（b-4）²=0.
1. （1）试求a、b的值，并求第三边c的取值范围；
2. （2）若△ABC是等腰三角形，试求此三角形的周长．
答案解析收藏纠错 + 选题
22. (2023八上·安吉期中) 某游乐场部分平面图如图所示，点C、E、A在同一直线上，点D、E、B在同一直线上，DB⊥AB．测得A处与E处的距离为80m，C处与E处的距离为40m，∠C＝90°，∠BAE＝30°．
1. （1）请求出旋转木马E处到出口B处的距离；
2. （2）请求出海洋球D处到出口B处的距离；
3. （3）判断入口A到出口B处的距离与海洋球D到过山车C处的距离是否相等？若相等，请证明；若不相等，请说明理由．
答案解析收藏纠错 + 选题
23. (2023八上·安吉期中) 如图，B为∠A边上一点，AB=5，BC⊥AC，P为线段AC上一点，点Q，P关于直线BC对称，QD⊥AB于点D，直线DQ，BC交于点E，连结DP，设AP=m.
1. （1）若BC=4，求用含m的代数式表示PQ的长；
2. （2）在（1）的条件下时，若AP=PD，求CP的长；
3. （3）连结PE，若∠A=60°，△PCE与△PDE的面积之比为1：2，求m的值.
答案解析收藏纠错 + 选题
24. (2023八上·安吉期中) 【发现问题】小强在一次学习过程中遇到了下面的问题：如图①，AD是△ABC的中线，若AB=5，AC=3，求AD的取值范围.
1. （1）【探究方法】
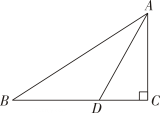
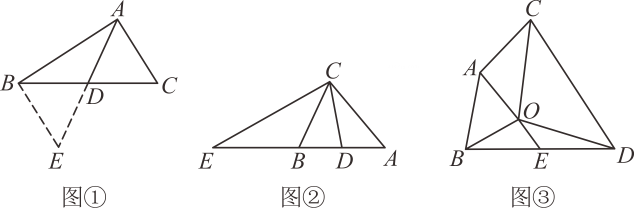
  小强所在的小组通过探究发现，延长AD至点E使ED=AD，连接BE.
  可以证出△ADC≌△EDB，利用全等三角形的性质可将已知的边长与AD转化到到△ABE中，进而求出AD的取值范围.
  方法小结：从上面的思路可以看出，解决问题的关键是将中线AD延长一倍，构造出全等三角形，我们把这种方法叫做“倍长中线法”.
  请你利用上面解答问题的思路方法，求出求AD的取值范围的过程.
2. （2）【问题解决】
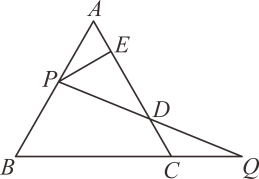
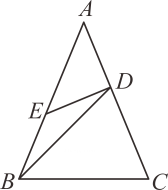
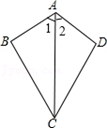
  如图②，CB是△AEC的中线，CD是△ABC的中线，且AB=AC，下列四个选项中：A．AC=BE B．CE=2CD C．∠BCD=∠BCE D．∠ACD=∠BCD.直接写出所有正确选项的序号是.
3. （3）【问题拓展】
  如图③，在△ABO和△CDO中，OA=OB，OC=OD，∠AOB与∠COD互补，连接AC、BD，E是BD的中点，求证：OE= $\text{[math]}$ AC.
答案解析收藏纠错 + 选题