浙江省金华市东阳市横店八校联考试卷2023-2024学年九年...

更新时间：2024-02-26 浏览次数：24 类型：月考试卷

一、选择题：本大題有10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. (2023九上·东阳月考) 已知⊙O的半径为2，点P在⊙O内，则OP的长可能是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
2. (2023九上·东阳月考) 关于二次函数y=3(x-2)²+1图象的说法，正确的是（）

A . 开口向下 B . 顶点坐标足(-2，1) C . 有最小值y=1 D . 对称轴是直线x=-2

答案解析收藏纠错 + 选题
3. (2023九上·东阳月考) 有九张背面相同的卡片，正面从1到9分别写有一个自然数．若卡片背面朝上，从中任意抽出一张，正面的数是奇数的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
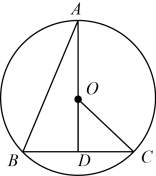
4. (2023九上·东阳月考) 如图是雨水管示意图，截面是半径为50cm的圆，管内水面AB=80cm，则水深CD等于（）(单位：cm)

A . 10 $\text{[math]}$ B . 10 $\text{[math]}$ C . 20 D . 30

答案解析收藏纠错 + 选题
5. (2023九上·东阳月考) 如图，△ABC内接于半径为2的⊙O．若∠A=45°，则 $\text{[math]}$ 的长等于（）

A . $\text{[math]}$ π B . $\text{[math]}$ π C . π D . 2π

答案解析收藏纠错 + 选题
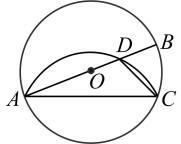
6. (2023九上·东阳月考) 如图，在⊙O中，AB为直径，点C为圆上一点，将劣弧 $\text{[math]}$ 沿弦AC翻折交AB于点D(不与O重合)，连结CD．若∠A=22°，则∠ACD的度数为（）

A . 46° B . 44° C . 48° D . 68°

答案解析收藏纠错 + 选题
7. (2023九上·东阳月考) 某同学在用列表描点法画二次函数y=ax²+bx+c的图糸时，列出了下面的表格：那么当x=5时，y的值为（）
x
……
-1
0
1
2
3
……
y
……
8
3
0
-1
0
……

A . 8 B . 6 C . 4 D . 3

答案解析收藏纠错 + 选题
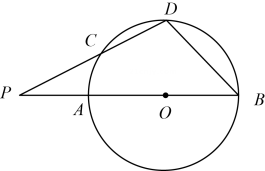
8. (2023九上·东阳月考) 如图，AB为⊙O的直径，P为BA延长线上的一点，D在⊙O上(不与点A，点B重合)，连结PD交⊙O于点C，且PC=OB．设∠P=α，∠B=β，下列说法正确的是（）

A . α+β=90° B . 3α+2β=180° C . 5α+4β=180° D . β-α=30°

答案解析收藏纠错 + 选题
9. (2023九上·东阳月考) 如图，已知⊙O的半径为4，直径AB垂直于弦CD，垂足为点E．若∠B=22.5°，则CD长度为（）

A . $\text{[math]}$ B . 4 C . $\text{[math]}$ D . 8

答案解析收藏纠错 + 选题
10. (2023九上·东阳月考) 已知二次函数y=a(x-1)(x-a)(a为常数，且a≠0)，下列结论一定正确的是（）

A . 若a>0，则 $\text{[math]}$ <x<a时，y随x的增大而增大 B . 若a>0，则 $\text{[math]}$ <x<a时，y随x的增大而减小 C . 若a<0，则a<x< $\text{[math]}$ 时，y随x的增大而增大 D . 若a<0，则a<x< $\text{[math]}$ 时，y随x的增大而减小

答案解析收藏纠错 + 选题

二、填空题：本大题有6个小题，每小题4分，共24分．

11. (2023九上·东阳月考) 投掷一枚均匀的立方体骰子，标有六点的面朝上的概率是.

答案解析收藏纠错 + 选题
12. (2023九上·东阳月考) 二次函数y=2x²-8x+1(0≤x≤3)的最小值是，最大值是.

答案解析收藏纠错 + 选题
13. (2023九上·东阳月考) 若抛物线y=ax²+bx与x轴的一个交点坐标为(-3，0)，则该抛物线的对称轴为直线.

答案解析收藏纠错 + 选题
14. (2023九上·东阳月考) 如图，BC是⊙O的弦，AD过圆心O，且AD⊥BC，若∠C=40°，则∠A的度数为.

答案解析收藏纠错 + 选题
15. (2023九上·东阳月考) 若点A( $\text{[math]}$ ， y₁)，B(-1，y₂)，C( $\text{[math]}$ ， y₃)为二次函数y=-ax²-4ax+5(a<0)图象上的三个点，则y₁ ， y₂ ， y₃的大小关系是.

答案解析收藏纠错 + 选题
16. (2023九上·滨江月考) 如图，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的半径为．

答案解析收藏纠错 + 选题

三、解答题：本大题有8个小题，共66分．解答应写出文字说明、证明过程或演箅步骤．

17. (2023九上·东阳月考) 已知y关于x的二次函数的部分函数值如列表所示：
x
-1
0
1
4
y
2
3
6
m
1. （1）求该二次函数解析式．
2. （2）求m的值．
答案解析收藏纠错 + 选题
18. (2023九上·东阳月考) 已知P（-5，m）和Q（3，m）是二次函数y=2x²+bx+1图象上的两点．
1. （1）求b的值；
2. （2）将二次函数y=2x²+bx+1的图象进行一次平移，使图象经过原点.（写出一种即可）
答案解析收藏纠错 + 选题
19. (2023九上·东阳月考) 在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的球．其中红球3个，白球5个，黑球若干个，若从中任意摸出一个白球的概率是 $\text{[math]}$
1. （1）求任意摸出一个球是黑球的概率：
2. （2）小明从盒子里取出m个白球(其他颜色球的数量没有改变)，使得从盒子里任意摸出一个球是红球的概率为 $\text{[math]}$ ，请求出m的值．
答案解析收藏纠错 + 选题
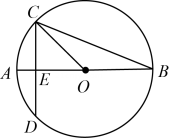
20. (2023九上·东阳月考) 如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8，AE=2．
1. （1）求⊙O的半径：
2. （2）求O到弦BC的距离．
答案解析收藏纠错 + 选题
21. 如图，在 $\text{[math]}$ 中，弦 $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，已知 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）如果 $\text{[math]}$ 的半径为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
22. (2023九上·东阳月考) 某公司投入研发费用80万元(80万元只计入第一年成本)，成功研发出一种产品，公司按订单生产(产量=销售量)，第一年该产品正式投产后，生产成本为6元/件，该产品定价8元/件时，销售量达到18万件，据测算售价每增加1元，销量将减少1万件．设此产品年销售量为y(万件)，售价为x(元/件)．
1. （1）求y与．x之间的函数关系式．
2. （2）设利润为w，求w与x的函数关系。如何定价时，年利润最大，最大是多少？
答案解析收藏纠错 + 选题
23. (2023九上·东阳月考) 在平面直角坐标系中，二次函数y=ax²-2ax+2(a<0)的图象与y轴交于点A．
1. （1）求点A的坐标及抛物线的对称轴．
2. （2）当0≤x≤3时，y的最大值是3，求当0≤x≤3时，y的最小值；
3. （3）抛物线上的两点P(x₁ ， y₁)，Q(x₂ ， y₂)，若对于t<x₁<t+1，t+2<x₂<t+3，都有y₁≠y₂ ，直接写出t的取值的范围．
答案解析收藏纠错 + 选题
24. (2023九上·东阳月考) 已知四边形ABCD，⊙O经过B，D两点，与四条边分别交于点E，F，G，H，且 $\text{[math]}$ = $\text{[math]}$ ．
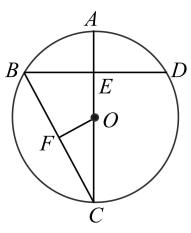
1. （1）如图①，连接BD，若BD是⊙O的直径，求证：∠A=∠C．
2. （2）如图②，若 $\text{[math]}$ 的度数为θ，∠A=α，∠C=β，请写出θ，α和β之间的数量关系，并说明理由．
答案解析收藏纠错 + 选题