吉林省长春市赫行实验学校2023-2024学年八年级上学期数...

更新时间：2023-12-27 浏览次数：30 类型：月考试卷

一、选择题（本大题共8小题，每小题3分，共24分）

1. (2024八上·南海月考) 下列实数中，属于无理数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3.14 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八上·长春月考) m⁶可以写成（）

A . m³·m² B . m²·m⁴ C . m·m⁶ D . m³+m³

答案解析收藏纠错 + 选题
3. (2023八上·长春月考) 下列命题中，属于假命题的是（）

A . 对顶角相等 B . 全等三角形对应边上的高相等 C . 同位角相等，两直线平行 D . 有三个角分别对应相等的两个三角形全等

答案解析收藏纠错 + 选题
4. (2023八上·长春月考) △ABC的三边长分别为a，b，c，下列条件不能判断△ABC是直角三角形的为（）

A . ∠A：∠B：∠C=3： 4： 5 B . ∠A=∠B-∠C C . a：b：c=3：4：5 D . a²=b²+c²

答案解析收藏纠错 + 选题
5. (2023八上·长春月考) 如图，已知∠1=∠2，要使△ABD≌△ABC，还需要添加一个条件，这个条件不可以是（）

A . ∠D=∠C B . ∠ABD=∠ABC C . AD=AC D . BD=BC

答案解析收藏纠错 + 选题
6. (2023八上·长春月考) 如图是一所学校对学生上学方式进行调查后，根据调查结果绘制了一个不完整的统计图，其中“其他”部分所对的圆心角度数是36°则步行部分所占的百分比是（　　）

A . 36% B . 40% C . 45% D . 50%

答案解析收藏纠错 + 选题
7. (2023八上·长春月考) 如图，用直尺和圆规作∠MAN的角平分线，根据作图痕迹，下列结论不一定正确的是（　　）

A . AD＝AE B . AD＝DF C . DF＝EF D . AF⊥DE

答案解析收藏纠错 + 选题
8. (2023八上·长春月考) 如图，在3×3的正方形网格中，每个小正方形边长为1，点A，B，C，D均为格点，以A为圆心，AB长为半径作弧，交网格线CD于点E，则C，E两点间的距离为（）

A . $\text{[math]}$ B . 3- $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ - $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分）

9. (2024七下·曲靖月考) 4的算术平方根是．

答案解析收藏纠错 + 选题
10. (2023八上·长春月考) 计算：（4a-b）²= ．

答案解析收藏纠错 + 选题
11. (2023八上·长春月考) 用反证法证明，“在△ABC中，∠A、∠B对边是a、b．若∠A<∠B，则a<b．”第一步应假设.

答案解析收藏纠错 + 选题
12. (2023八上·长春月考) 某中学新建食堂正式投入使用，为提高服务质量，食堂管理人员对学生进行了“最受欢迎菜品”的调查统计，以下是打乱了的调查统计顺序，请按正确顺序重新排序（只填序号）
①绘制扇形图；
②收集最受学生欢迎菜品的数据；
③利用扇形图分析出受欢迎的统计图；
④整理所收集的数据．

答案解析收藏纠错 + 选题
13. (2023八上·长春月考) 如图，在△ABC中，AB，AC的垂直平分线分别交BC于点D，E，垂足分别为M，N，已知△ADE的周长为22，则BC的长为

答案解析收藏纠错 + 选题
14. (2023八上·长春月考) “三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任意一个角。这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D、E可在槽中滑动．若∠BDE=75°，则∠CDE的度数是

答案解析收藏纠错 + 选题

三、解答题（本大题共10小题，共78分）

15. (2023八上·长春月考) 计算：
1. （1）（x²）³÷x⁵
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
16. (2023八上·长春月考) 因式分解：
1. （1） a³-4a
2. （2） 3mx²-6mxy+3my²
答案解析收藏纠错 + 选题
17. (2023八上·长春月考) 先化简，再求值：（2x-1）²+（3+2x）（3-2x），其中x=1．

答案解析收藏纠错 + 选题
18. (2023八上·长春月考) 如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画图形．
1. （1）在图1中，画一个直角三角形，使它的三边长都是有理数；
2. （2）在图2中，画一个等腰三角形，使它的面积为8；
3. （3）在图3中，画一个等腰直角三角形，使它的面积为5．
答案解析收藏纠错 + 选题
19. (2023八上·长春月考) 如图，已知AB⊥BC，AD⊥DC，AB=AD．求证：∠1=∠2．
1. （1）求证：∠1=∠2
2. （2）若∠1=56°，则∠BCD= °
答案解析收藏纠错 + 选题
20. (2023八上·长春月考) 某校八年级的王明和孙亮两位同学在学习了“勾股定理”之后，为了测得风筝的垂直高度CE，他们进行了如下操作：
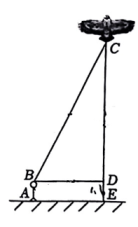
①测得BD的长度为8米；（注：BD⊥CE）
②根据手中剩余线的长度计算出风筝线BC的长为17米：
③牵线放风筝的王明身高AB=1.6米：（注：AB=DE）
求风筝的垂直高度CE；

答案解析收藏纠错 + 选题
21. (2023八上·长春月考) 随着双减政策的落实，同学们的家庭作业减少了．为了解同学们完成家庭作业需要的时间，某校数学兴趣小组随机调查了部分学生（问卷调查的内容如图1所示），并根据调查结果绘制了如图2所示的尚不完整的统计图．
家庭作业您用了多长时间？（单选）
A不用在家写作业B20分钟以内 C.40分钟以内D.60分钟以内E.60分钟以上
1. （1）本次接受调查的学生共有人；
2. （2）请补全条形统计图：
3. （3）求被调查的学生中，完成家庭作业时间不超过40分钟的学生人数占总调查人数的百分比．
答案解析收藏纠错 + 选题
22. (2023八上·长春月考) 感知：如图①，△ABC和△AED都是等腰直角三角形，∠BAC=∠DAE=90°，点B在线段AD上，点C在线段AE上，我们很容易得到BD=CE，不需证明．
1. （1）探究：如图②，将△AED绕点A逆时针旋转a （0<a<90° ），连结BD和CE，此时BD=CE是否依然成立？若成立，写出证明过程；若不成立，说明理由．
2. （2）应用：如图③，△ADE绕点A逆时针旋转，使得点D落在BC的延长线上，连结CE．
  ①∠ACE的度数为度；
  ②线段BD、CD、ED之间的数量关系是 .
答案解析收藏纠错 + 选题
23. (2023八上·长春月考) 数学课时，老师在讲完乘法公式（a±b）²=a²±2ab+b²的多种运用后，要求同学们运用所学知识解答：求代数式x²+4x+5的最小值？同学们经过交流、讨论，最后总结出如下解答方法：
解： x²+4x+5=x²+4x+4+1= （x+2）²+1
∵（x+2）²≥0，
∴当x=-2时，（x+2）²的值最小，最小值是0，
∴（x+2）²+1≥1
∴当（x+2）²=0时，（x+2）²+1的值最小，最小值是1，
∴x²+4x+5的最小值是1．
请你根据上述方法，解答下列各题：
1. （1）知识再现：求x为何值时，代数式x²-4x+6有最小值，并求出这个值；
2. （2）知识运用：若y=-x²+4x+5，当x=时，y有最值（填“大”或“小”），这个值是
答案解析收藏纠错 + 选题
24. (2023八上·长春月考) 如图，在△ABC中，∠C=90°，AC=12，BC=5，BD平分∠ABC．动点P从点B出发，沿折线BA-AC以每秒1个单位长度的速度向点C运动，当点P不与点D重合时。连结P、B、D三点．设点P的运动时间为t秒（t>0}．
1. （1）线段AB的长为
2. （2）当点P在线段AB上运动时，线段BP=，AP=（均用含有t的式子表示）
3. （3）当△DBP的面积等于 $\text{[math]}$ 时，求出t的值；
4. （4）当△DBP是钝角三角形时，直接写出t的取值范围．
答案解析收藏纠错 + 选题