吉林省长春市第七十二中学2023-2024学年九年级上学期第...

更新时间：2023-12-30 浏览次数：26 类型：月考试卷

一、选择题（本大题共8小题，每小题3分，共24分）

1. (2023·广西壮族自治区模拟) -3的绝对值是（）

A . -3 B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九上·长春月考) 某企业一个项目的总投资为4 170 000元.4 170 000这个数用科学记数法表示为

A . 0.417×10⁷ B . 4.17×10⁶ C . 4.17×10⁷ D . 41.7×10⁵

答案解析收藏纠错 + 选题
3. (2023九上·长春月考) 不等式组 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023九上·长春月考) 将抛物线y=2（x-1）²-3先向右平移3个单位，再向下平移2个单位，平移后拋物线的顶点坐标为（）

A . （-2，-1） B . （-2，-5） C . （4，-1） D . （4，-5）

答案解析收藏纠错 + 选题
5. (2023九上·长春月考) 如图，某学校有一块长35米、宽20米的长方形试验田，为了便于管理，现要在中间开辟一横两纵三条等宽的小道，要使种植面积为600平方米．设小道的宽为x米，根据题意可列方程为（）

A . （35-x）（20-2x）=600． B . 35×20-35x-20x+2x²=600． C . （35-2x）（20-x）=600． D . 35x+2×20x-2x²=600．

答案解析收藏纠错 + 选题
6. (2023九上·长清期中) 如图，l₁∥l₂∥l₃ ，直线AC、DF与这三条平行线分别交于点A、B、C和点D、E、F，若AB＝4，DE＝3，EF＝6，则AC的长是（　　）

A . 4 B . 6 C . 8 D . 12

答案解析收藏纠错 + 选题
7. (2023九上·长春月考) 如图，在正方形ABCD中，点E在AB边上，AF⊥DE于点G，交BC于点F．若AB=15，BE=5，则△AEG的面积与四边形BFGE的面积之比是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·长春月考)
二次函数y=ax²+bx的图象如图，若一元二次方程ax²+bx+m=0有实数根，则m的最大值为（　　）

A . -3 B . 3 C . -6 D . 9

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分）

9. (2024八下·白云期末) 计算： $\text{[math]}$ =.

答案解析收藏纠错 + 选题
10. (2023九上·长春月考) 关于x的一元二次方程x²-5x+k=0有两个不相等的实数根，则k的取值范围是

答案解析收藏纠错 + 选题
11. (2023九上·长春月考) 《九章算术》是我国古代数学名著，书中有如下问题：“今有井径五尺，不知其深，立三尺木于井上，从木末望水岸，入径五寸．问井深几何？”意思是：如图，井径 $\text{[math]}$ 尺，立木高 $\text{[math]}$ 尺， $\text{[math]}$ 寸 $\text{[math]}$ 尺，则井深 $\text{[math]}$ 为尺．

答案解析收藏纠错 + 选题
12. (2023九上·长春月考) 如图，△ABC的顶点都在方格纸的格点上，则cosA=

答案解析收藏纠错 + 选题
13. (2023九上·长春月考) 如图，点E为矩形 $\text{[math]}$ 的 $\text{[math]}$ 边上一点，以 $\text{[math]}$ 为折痕将 $\text{[math]}$ 向上折叠，点B恰好落在 $\text{[math]}$ 边上的点F处，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
14. (2023九上·长春月考) 如图，在平面直角坐标系中，抛物线y=x²+4x+m与x轴交于点A、B，与y轴交于点C，过点C作CD∥x轴交抛物线于点D．若AB+CD=6，则抛物线的解析式为

答案解析收藏纠错 + 选题

三、解答题（本大题共10小题，共78分）

15. (2023九上·长春月考) $\text{[math]}$ +|1- $\text{[math]}$ |-2sin 45°

答案解析收藏纠错 + 选题
16. (2023九上·长春月考) 解方程：x²＋3x－1=0

答案解析收藏纠错 + 选题
17. (2023九上·长春月考) 有两个不透明的口袋，一个口袋装有2个红球、1个白球，另一个口袋装有1个黄球、2个红球，这些球除了颜色外其它完全相同．从两个口袋中各随机摸出1个球，用画树状图（或列表）的方法，求摸出的两个球颜色相同的概率．

答案解析收藏纠错 + 选题
18. (2023九上·长春月考) 某课外活动小组借助如图所示的直角墙角（两边足够长）用篱笆围成矩形花园ABCD，篱笆只围AB、BC两边，已知篱笆长为30m，篱笆围成的矩形ABCD的面积为225m² ，求边AB的长．

答案解析收藏纠错 + 选题
19. (2023九上·长春月考) 如图，小芳站在地面上A处放风筝，风筝飞到C处时的线长BC为23米，这时测得∠CBD=58°，牵引底端B与地面的距离BA为1.6米，求此时风筝离地面的高度CE．（结果精确到0.1米）
[参考数据：sin58°=0.85，cos58°=0.53， tan58°=1.60]

答案解析收藏纠错 + 选题
20. (2023九上·长春月考) 图①、图②、图③均是5×5的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，点A、B均在格点上，只用无刻度的直尺，分别在给定的网格中按下列要求作△ABC，点C在格点上．
1. （1）在图①中，△ABC的面积为 $\text{[math]}$ ，
2. （2）在图②中，△ABC的面积为5；
3. （3）在图③中，△ABC是面积为 $\text{[math]}$ 的钝角三形．
答案解析收藏纠错 + 选题
21. (2023九上·长春月考) 如图，隧道的截面由抛物线DEC和矩形ABCD构成，矩形的长AB为4m，宽BC为3m，以DC所在的直线为x轴，线段CD的中垂线为y轴，建立平面直角坐标系。y轴是抛物线的对称轴，最高点E到地面距离为4米．
1. （1）求出抛物线的解析式．
2. （2）在距离地面 $\text{[math]}$ 米高处，隧道的宽度是多少？
3. （3）如果该隧道内设单行道（只能朝一个方向行驶），现有一辆货运卡车高3.6米，宽2.4米，这辆货运卡车能否通过该隧道？通过计算说明你的结论．
答案解析收藏纠错 + 选题
22. (2023九上·长春月考) [教材呈现]如图是华师版九年级上册数学教材第103页的部分内容．
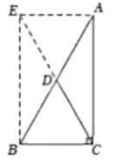
例2如图，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线．
求证：CD= $\text{[math]}$ AB．
证明：延长CD至点E，使DE=CD，连结AE、BE．
1. （1）请根据教材提示，结合图①，写出完整的证明过程．
2. （2） [结论应用]如图②，四边形ABCD中，∠BAD=90°，∠DCB=90°，E、F分别是BD、A的中点，当AC=4，BD=5时，则EF=
3. （3）如图③，BD是Rt△ABC斜边AC上的中线．AB=3，BC=4，点P是BC上一个点，过P分别作AC和BD的垂线，垂足为E、F．当P在BC上移动时，则PE+PF=
答案解析收藏纠错 + 选题
23. (2023九上·长春月考) 如图，在△ABC中，∠ACB=90°，AB=5，BC=3，动点P从点A出发，沿AC以每秒2个单位长度的速度向终点C匀速运动，设点P的运动时间为t秒（r>0）。过点P作AB的垂线交AB于点M．
1. （1） AC=
2. （2）求PM的长．（用含有t的代数式表示）
3. （3）若将点P绕点M逆时针旋转90于点N．
  ①求BN的长（用含t的代数式表示）
  ②在点P运动的同时，做点B关于点N的对称点Q，连结PQ．
  当△AQP为等腰三角形时，直接写出t的值．
答案解析收藏纠错 + 选题
24. (2023九上·长春月考) 在平面直角坐标系中，抛物线p=-x²+bx+c （b、c为常数）与x轴交点的坐标是（3，0），对称轴为直线x=1．
1. （1）求此抛物线所对应的二次函数的表达式，
2. （2）直接写出当x≥2，函数值y随x的增大而增大时y的取值范围，
3. （3）点A、点B均在这个抛物线上，点A的横坐标为a，点B的横坐标为4+a，将A、B两点之间的部分（包括A、B两点）记为图象G．
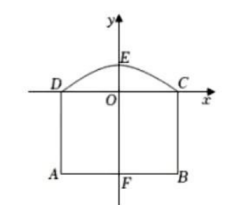
  ①当A、B两点纵坐标相等时，求AB中点的坐标。
  ②设图象G的最高点的纵坐标与最低点的纵坐标的差为h，求h与a的函数关系式，并写出a的取值范围．
答案解析收藏纠错 + 选题