
 B .
B .  C .
C .  D .
D . 



x2﹣2x﹣3=0


⑴画出△ABC关于y轴对称的图形△A1B1C1 , 写出C1点的坐标;
⑵以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2 , 写出C2点坐标;
为迎接“双十一”,该网店决定降价促销,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.

项目主题:测量旗杆高度

问题驱动:能利用哪些科学原理来测量旗杆的高度?
组内探究:由于旗杆较高,需要借助一些工具来测量,比如自制的直角三角形硬纸板,标杆,镜子,甚至还可以利用无人机…确定方法后,先画出测量示意图,然后实地进行测量,并得到具体数据,从而计算旗杆的高度.
成果展示:下面是同学们进行交流展示时的部分测量方案:
| 方案一 | 方案二 | … | ||
测量工具 | 标杆,皮尺 | 自制直角三角板硬纸板,皮尺 | … | ||
测量示意图 |
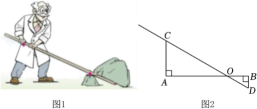
说明:线段AB表示学校旗杆,小明的眼睛到地面的距离CD=1.7m,测点F与B,D在同一水平直线上,D,F,B之间的距离都可以直接测得,且A,B,C,D,E,F都在同一竖直平面内,点A,C,E三点在同一直线上. |
说明:线段AB表示旗杆,小明的身高CD=1.7m,测点D与B在同一水平直线上,D,B之间的距离可以直接测得,且A,B,C,D,E,F,G都在同一竖直平面内,点A,C,E三点在同一直线上,点C,F,G三点在同一直线上. | |||
测量数据 | B,D之间的距离 | 16.8m | B,D之间的距离 | 16.8m | … |
D,F之间的距离 | 1.35m | EF的长度 | 0.50m | … | |
EF的长度 | 2.60m | CE的长度 | 0.75m | … | |
… | … | ||||
根据上述方案及数据,请你选择一个方案,求出学校旗杆AB的高度.(结果精确到0.1m);


①参加问卷调查的学生共有 人;
②扇形统计图中“D”对应扇形的圆心角的度数为 ;

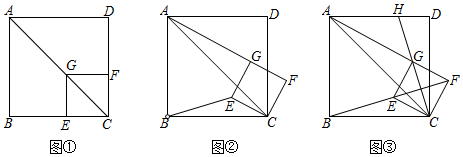
②推断:的值为 ▲ ;