吉林省白山市江源区三校名校调研系列卷2023-2024学年九...

更新时间：2024-01-08 浏览次数：42 类型：月考试卷

一、选择题（每小题2分，共12分}

1. (2023九上·江源月考) 下列图案中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023九上·江源月考) 若x=-2是一元二次方程x²+mx+2= 0的一个根，则m的值是（）

A . -3 B . -2 C . 2 D . 3

答案解析收藏纠错 + 选题
3. (2023九上·江源月考) 下列事件中，属于必然事件的是（）

A . 抛掷硬币时，正面朝上 B . 小明发烧了，体温达到50℃ C . 经过红绿灯路口，遇到红灯 D . 任意写一个负数，小于正数

答案解析收藏纠错 + 选题
4. (2023九上·江源月考) 关于二次函数y=-（x-3）²+2的最值，下列说法正确的是（）

A . 有最大值3 B . 有最小值3 C . 有最大值2 D . 有最小值2

答案解析收藏纠错 + 选题
5. (2023九上·江源月考) 如图，在平面直角坐标系中，△ABC绕点C（0，1）旋转180°得到△A'B'C，已知点A的坐标为（2，-1）．则点A'的坐标是．（）

A . （- 2，1） B . （-2，3） C . （-2，-1） D . （-2，2）

答案解析收藏纠错 + 选题
6. (2023九上·江源月考) 如图，A、B、C是⊙O上的三个点，∠ABC=50°，连接AO、OC．过点O作OD⊥BC 于点D．若∠OCD=40°，则∠AOD的度数为（）．

A . 120° B . 135° C . 140° D . 150°

答案解析收藏纠错 + 选题

二、填空题（每小题3分，共24分）

7. (2023九上·江源月考) 方程x（4-x）=0的解为

答案解析收藏纠错 + 选题
8. (2023九上·江源月考) 抛物线y= （x-5）²+5的顶点坐标是

答案解析收藏纠错 + 选题
9. (2023九上·江源月考) 已知⊙O的半径为4cm，OP =2cm，则点P在⊙O（填“内"、“外”或“上”）．

答案解析收藏纠错 + 选题
10. (2023九上·江源月考) 如图，该图形绕其中心旋转能与自身完全重合．则其旋转角最小为度．

答案解析收藏纠错 + 选题
11. (2023九上·江源月考) 将抛物线y=3（x-1）²+2向左平移3个单位长度，得到的新抛物线的解析式为

答案解析收藏纠错 + 选题
12. (2023九上·江源月考) 张师傅去华开了一家超市，今年2月份开始盈利，3月份盈利5000元，5月份盈利达到7200元，从3月到5月，设每月盈利的平均增长率都是x．则根据题意。可列方程：

答案解析收藏纠错 + 选题
13. (2023九上·江源月考) 如图．二次函数y=ax²+bx+c的图象与x轴交于点（3，0），对称轴是直线上x= 1．则当y<0时。自变量x的取值范围是

答案解析收藏纠错 + 选题
14. (2023九上·江源月考) 如图，点C、D是⊙O上直径AB两侧的两点，若∠ACD= 60°．AB=8．则 $\text{[math]}$ 的长为（结果保留π）．

答案解析收藏纠错 + 选题

三、解答题（每小题5分，共20分）

15. (2023九上·江源月考) 解方街：x²+ 10x+24 = 3．

答案解析收藏纠错 + 选题
16. (2023九上·江源月考) 已知抛物线的顶点A（1，-4）．且经过点B（3，0）．求该抛物线的解析式：

答案解析收藏纠错 + 选题
17. (2023九上·江源月考) 如图，在△ABC中，AB=2，BC=3.6．∠B=60°，将△ABC绕点A按顺时针方向旋；转一定角度得到△ADK，当点B的对应点D恰好落在BC边上时，求CD的长．

答案解析收藏纠错 + 选题
18. (2023九上·江源月考) 如图，AB是⊙O的一条弦，点C是AB的中点，连接OC并延长交 $\text{[math]}$ 于点D，连接OB、DB．若AB=4．CD=1．求△BOD的面积．

答案解析收藏纠错 + 选题

四、解答题{每小题7分，共28分}

19. (2023九上·江源月考) 如图是四张不透明的卡片．除正面分别有数字1、1、2、3 外．其他均相间．将这四张卡肯面朝上洗匀后放置在桌面上．
1. （1）小明从中随机抽取一张卡片，恰好得到数字1的概率是．
2. （2）小明和小丽恕用这四张卡片做游戏，游戏规则为小明先随机抽取一张卡片，小丽再从余下的卡片中随机抽取一张．如朵两张卡片上的数字和为奇数，小明胜；和为偶数，小丽胜．你认为这个游戏公平吗？请用列表或画树状图的方法说明理由．
答案解析收藏纠错 + 选题
20. (2023九上·江源月考) 光明中学准备在校园里利用围墙（墙长15m）和45m长的篱笆墙围建劳动实践基地．该校某数学兴趣小组设计了如下的围建方案（除围墙外，实线部分均为篱笆墙，且不浪费篱笆墙）：利用围墙和篱笆墙围成Ⅰ、Ⅱ两块矩形劳动实践基地，且在Ⅱ区中留一个宽度EH=1m的水池EFBH．已知CG=2DG．设DG的长度为xm．
1. （1） AD的长度为m（用含x的代数式表示）；
2. （2）若劳动基地的总面积（不包含水池）为124m² ，求DG的长是多少？
答案解析收藏纠错 + 选题
21. (2023九上·江源月考) 如图。四边形ABCD内接于⊙O，BC为⊙O的直径。OA∥CD．
1. （1）若∠ABC=70°，求∠BAD的度数；
2. （2）求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2023九上·江源月考) 如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（-1，0）．B（-4，1）．C（-2，2）．
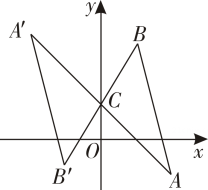
⑴直接写出点B关于原点O对称的点B₁的坐标；
⑵请画出△ABC关于原点O成中心对称的△A₂B₂C₂ ．
⑶画出△ABC绕点A逆时针旋转90°后得到的△AB₃C₃ ．

答案解析收藏纠错 + 选题

五、解答题{每小题8分，共16分}

23. (2023九上·江源月考) 如图。AB是⊙O的直径，AP是⊙O的切线。点A为切点．BP与⊙O交于点C，点D是AP的中点。连接CD．
1. （1）求证：CD是⊙O的切线：
2. （2）若AB=2，∠P=30°，求阴影部分的面积（结果保留根号和π）．
答案解析收藏纠错 + 选题
24. (2023九上·江源月考) 如图①．四边形ABCD与四边形AEFG是共一个顶点的两个大小不同的正方形．
1. （1）操作发现：如图②．正方形AEFG绕顶点A逆时针旋转，使点E落在边AD上时．填空：
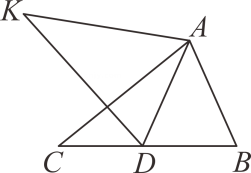
  ①线段BE与IG的数量关系是
  ②∠ABE与∠ADG的关系是
2. （2）猜想与证明：如图③，正方形AEFG绕顶点A逆时针旋转某一角度α（0<α< 90°）时．猜想（1）中的结论是否成立？并证明你的结论：
3. （3）拓展应用：如图④．正方形AEFG绕顶点A逆时针旋转，使点F落在边AD上时，若AB= $\text{[math]}$ ． AF=1，则BE=
答案解析收藏纠错 + 选题

六、解答题（每小题10分，共20分）

25. (2023九上·江源月考) 如图。在Rt△ABC中，∠C=90°．AC=BC，AB=4，点D为AB的中点．动点P从
点A出发沿线段AB以每秒1个单位长度的速度向终点B运动，点P关于点D中心对称的点为点Q．当点P与点D不重合时，以PQ为直角边向PQ上方作等腰直角△QPM．使∠QPM=90°．设点P的运动时间为t秒．
1. （1）用含t的代数式表示线段PQ的长（直接写出）；
2. （2）当点M落在△ABC的边上时，求t的值；
3. （3）当△PQM与△ABC重叠部分为四边形时，求重叠部分的面积S与t之间的函数关系式．
答案解析收藏纠错 + 选题
26. (2023九上·江源月考) 如图，抛物线的顶点坐标为（2，6），且经过点（4，2）．点P是第一象限内的抛物线上的一点．且在对称轴右侧．过点P作PM⊥x轴于点M．PN⊥y轴于点N．设点P的横坐标为m．
1. （1）求这条抛物线对应的函数解析式
2. （2）当四边形OMPN为正方形时，求m的值
3. （3）求四边形OMPN的周长的最大值
4. （4）若直线PN与这条抛物线的另一个交点为点Q，直接写出当 $\text{[math]}$ 时m的取值范围．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

吉林省白山市江源区三校名校调研系列卷2023-2024学年九...

副标题：

*注意事项：

吉林省白山市江源区三校名校调研系列卷2023-2024学年九...

试题分析

总体分析

题量分析

难度分析

知识点分析