浙江省绍兴市浣江教育共同体2023-2024学年八年级上学期...

更新时间：2024-03-22 浏览次数：45 类型：期中考试

一、选择题（本题有10小题，每小题3分，共30分）

1. (2023八上·萧山月考) 2023年第19届亚运会是一场规模盛大的体育盛事，下列体育图标是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023八上·绍兴期中) 以下列数组作为三角形的三条边长，其中能构成直角三角形的是（）

A . 1， $\text{[math]}$ ，3 B . $\text{[math]}$ ， $\text{[math]}$ ，5 C . 1.5，2，2.5 D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023八上·绍兴期中) 如图，小明书上的三角形被墨迹遮挡了一部分，但他很快想到办法在作业本上画了一样的三角形，那么这两个三角形完全一样的依据是（）

A . AAS B . ASA C . SSS D . SAS

答案解析收藏纠错 + 选题
4. (2023八上·绍兴期中) 若 $\text{[math]}$ ，则下列不等式不成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八上·绍兴期中) 一副三角板如图摆放，则 $\text{[math]}$ 的值是（）

A . 125° B . 100° C . 115° D . 105°

答案解析收藏纠错 + 选题
6. (2023八上·绍兴期中) 对于命题“若 $\text{[math]}$ ，则 $\text{[math]}$ ”，下面四组关于x，y的值中，能说明这个命题是假命题的是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023八上·绍兴期中) 已知等腰三角形ABC的底边 $\text{[math]}$ cm，且 $\text{[math]}$ cm，那么△ABC的周长为（）

A . 12cm B . 12cm或24cm C . 24cm D . 12cm或21cm

答案解析收藏纠错 + 选题
8. (2023八上·绍兴期中) 如图，一平面镜以与水平面成45°角固定在水平面上，一小球以1m/s的速度沿桌面向点O匀速滚去，则小球在平面镜中的像是（）

A . 以1m/s的速度，做竖直向下运动 B . 以1m/s的速度，做竖直向上运动 C . 以2m/s的速度运动，且运动路线与地面成45°角 D . 以2m/s的速度，做竖直向下运动

答案解析收藏纠错 + 选题
9. (2023八上·绍兴期中) 如图，AD是△ABC的高，以点B为圆心，适当长为半径画弧交AB于点M，交BC于点N；分别以M，N为圆心，以大于 $\text{[math]}$ 的长为半径画弧交于点P；作射线BP交AD于点E．若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则CD的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023八上·绍兴期中) 我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”，如图是由弦图变化得到，它是用八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ ，则下列关于 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的说法正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本题有10小题，每小题3分，共30分）

11. (2024七下·安溪期中) $\text{[math]}$ 的2倍与5的差是负数，用不等式表示为.

答案解析收藏纠错 + 选题
12. (2024七下·天桥期中) 在 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$ 是（填入“锐角三角形”、“直角三角形”或“钝角三角形”）

答案解析收藏纠错 + 选题
13. (2023八上·绍兴期中) 若直角三角形斜边上的中线长为5，则此直角三角形斜边长为．

答案解析收藏纠错 + 选题
14. (2023八上·绍兴期中) 如图，一棵树在一次强台风中在离地面 $\text{[math]}$ 米处折断倒下，倒下部分与地面成 $\text{[math]}$ 的夹角，树尖离树根的水平距离是 $\text{[math]}$ 米，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2023八上·绍兴期中) 如图，在△ABC中， $\text{[math]}$ ， ∠ABC和∠ACB的平分线分别交ED于点G、F，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
16. (2023八上·绍兴期中) 若一个等腰三角形一个内角是另一个内角的一半，则此三角形底角度数为．

答案解析收藏纠错 + 选题
17. (2024八上·温州期中) 已知关于x的不等式组 $\text{[math]}$ 无解，则a的取值范围为．

答案解析收藏纠错 + 选题
18. (2023八上·绍兴期中) 如图，在等腰Rt△ABC中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， D、E分别是边BC，AC上的点，将DE绕点D顺时针旋转90°，点E刚好落在边AB上的点F处，则CE的长为．

答案解析收藏纠错 + 选题
19. (2023八上·绍兴期中) 如图，∠AOB=30°，点D为∠AOB平分线OC上一点，OD的垂直平分线交OA、OB分别于点P，Q，点E是OA上异于点P的一点，且DE=OP=6，则△ODE的面积为.

答案解析收藏纠错 + 选题
20. (2023八上·绍兴期中) 如图，在△ABC中， $\text{[math]}$ ， $\text{[math]}$ ， D是AB边上的一个动点，点E与点A关于直线CD对称，当△ADE为直角三角形时，则AD的长为．

答案解析收藏纠错 + 选题

三、解答题（本题有6小题，第21-25题每小题6分，第26题10分，共40分）

21. (2023八上·绍兴期中) 解不等式组，并把解集在数轴上表示出来： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
22. (2023八上·绍兴期中) 如图，△ABC是格点三角形．
图1 图2
①在图1中画出一个与△ABC全等且有一条公共边BC的格点三角形；
②在图2中画出一个与△ABC全等且有一个公共点A的格点三角形．

答案解析收藏纠错 + 选题
23. (2023八上·绍兴期中) “剧本杀”作为新的娱乐形式受到青年人的追捧，喵喵“剧本杀”为扩大经营欲购进“青春学园”和“未来纪元”两种剧本配套设备，已知购买一套“青春学园”和两套“未来纪元”设备共需1450元，购买两套“青春学园”和一套“未来纪元”设备共需1700元．
1. （1）间“青春学园”和“未来纪元”设备的单价各为多少元？
2. （2）根据经营情况，需要购买“青春学园”和“未来纪元”设备共计20套，且总费用不超过10000元，则最多可购买“青春学园”设备多少套？
答案解析收藏纠错 + 选题
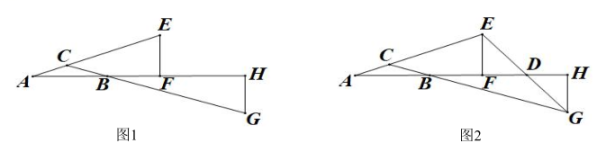
24. (2023八上·绍兴期中) 如图1：△ABC中， $\text{[math]}$ ，延长AC到E，过点E作 $\text{[math]}$ 交AB的延长线于点F，延长CB到G，过点G作 $\text{[math]}$ 交AB的延长线于H，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）如图2，连接EG与FH相交于点D，若 $\text{[math]}$ ，求DH的长．
答案解析收藏纠错 + 选题
25. (2023八上·绍兴期中) 如图1：正方形ABCD的边长为3，E是直线AD上一动点，连接CE，在CE的右侧以C为直角顶点作等腰直角三角形ECF，连接BE，DF．
1. （1）当点E在线段AD上运动时，试判断BE与DF的数量关系，并说明理由．
2. （2）当 $\text{[math]}$ 时，求DF的长．
3. （3）如图2，连接BF，则 $\text{[math]}$ 的最小值为．
答案解析收藏纠错 + 选题
26. (2023八上·绍兴期中) 如图，△ABC是边长为6cm的等边三角形，点P，Q分别从顶点A，B同时出发，点P沿射线AB运动，点Q沿折线 $\text{[math]}$ 运动，且它们的速度都为1cm/s．当点Q到达点A时，点P随之停止运动．连接PQ，PC，设点P的运动时间为t（s）．
1. （1）当点Q在线段BC上运动时，BQ的长为（cm），BP的长为（cm）（用含t的式子表示）．
2. （2）当PQ与△ABC的一条边垂直时，求t的值．
3. （3）当点Q从点C运动到点A的过程中，连接PQ，直接写出PQ中点O经过的路径长．
答案解析收藏纠错 + 选题