一、单选题(本题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,一个选项符合要求,选对得5分,错选得0分.)
-
-
-
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
-
-
-
-
-
二、多项选择题(本题共4个小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项符合要求.全部选对得5分,部分选对得2分,错选得0分.)
-
A . 不等式 恒成立
B . 存在
恒成立
B . 存在 , 使得不等式
, 使得不等式 成立
C . 若
成立
C . 若 , 则
, 则 D . 若正实数
D . 若正实数 满足
满足 , 则
, 则
-
-
A .  B .
B .  ,
,  C .
C .  有最大值
D .
有最大值
D .  最小值为0
最小值为0
-
A .  在
在 上为减函数
B .
上为减函数
B .  的最大值是1
C .
的最大值是1
C .  的图象关于直线
的图象关于直线 对称
D .
对称
D .  在
在 上
上
三、填空题(本题共4小题,每题5分,共20分)
-
-
-
-
16.
(2023·东莞期中)
定义:函数

在区间

上的最大值与最小值的差为

在区间

上的极差,记作

.
①若 , 则
, 则 ;
;
②若 , 且
, 且 , 则实数
, 则实数 的取值范围是.
的取值范围是.
四、解答题(本大题共6小题,第17题10分,18、19、20、21、22题各12分,共70分.解答应写出文字说明、证明过程或演算步骤.)
-
-
(1)
若

, 求

-
(2)
若

, 求实数m的取值范围.
-
-
(1)
求幂函数

的解析式;
-
(2)
若函数

, 根据定义证明

在区间

上单调递增.
-
-
-
(2)
若

, 求

的取值范围.
-
-
(1)
若

, 且关于x的不等式

的解集是

, 求

的最小值;
-
-
21.
(2023·东莞期中)
某企业为积极响应国家垃圾分类号召,在科研部门的支持下进行技术创新,新上一个把厨余垃圾加工处理为可重新利用的化工产品的项目.已知该企业日加工处理量x(单位:吨)最少为70吨,最多为100吨.日加工处理总成本(单位:元)与日加工处理量x之间的函数关系可近似地表示为

, 且每加工处理1吨厨余垃圾得到的化工产品的售价为110元.
-
(1)
该企业日加工处理量为多少吨时,日加工处理每吨厨余垃圾的平均成本最低?此时该企业处理1吨厨余垃圾处于亏损还是盈利状态?
-
(2)
为了使该企业可持续发展,政府决定对该企业进行财政补贴,补贴方案共有两种:
①每日进行定额财政补贴,金额为2300元;
②根据日加工处理量进行财政补贴,金额为 元.如果你是企业的决策者,为了获得最大利润,你会选择哪种补贴方案?为什么?
元.如果你是企业的决策者,为了获得最大利润,你会选择哪种补贴方案?为什么?
-
-
(1)
判断

的奇偶性;
-
(2)
判断函数单调性,求

在区间

上的最大值;
-
 B .
B . 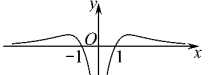 C .
C . 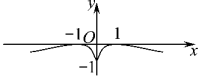 D .
D . 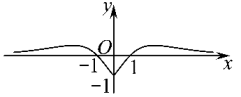
元.如果你是企业的决策者,为了获得最大利润,你会选择哪种补贴方案?为什么?