【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻...

更新时间：2023-12-12 浏览次数：46 类型：复习试卷

一、选择题

1. 下列说法正确的是（）．

A . 相似图形一定是位似图形 B . 位似图形不一定是相似图形 C . 全等图形不可能是位似图形 D . 位似图形一定是相似图形

答案解析收藏纠错 + 选题
2. 下列图形中，不属于位似图形的是（）.

A . B . C . D .

答案解析收藏纠错 + 选题
3. 以原点 $\text{[math]}$ 为位似中心，作 $\text{[math]}$ 的位似图形 $\text{[math]}$ 与 $\text{[math]}$ 的位似比为3.若点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为（）.

A . $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
4. 用图形的位似把图形扩大或缩小时，下列说法中，正确的是（）.

A . 位似中心要么取在图形的外部，要么取在图形的内部 B . 位似中心取在图形的内部时，只能把图形缩小 C . 当位似中心确定后，按要求放大或缩小的图形只能画一个 D . 以上说法都不正确

答案解析收藏纠错 + 选题
5. (2022九上·平阳月考) 如图，已知△ABC与△DEF是位似图形，O是位似中心，若OA＝2OD，则△ABC与△DEF的周长之比是（）

A . 2：1 B . 3：1 C . 4：1 D . 6：1

答案解析收藏纠错 + 选题
6. (2022·温州模拟) 如图，四边形ABCD与四边形AEFG是位似图形，位似比为3∶2.若EF=6，则BC的长为（）

A . 8 B . 9 C . 10 D . 15

答案解析收藏纠错 + 选题
7. (2023·舟山模拟) 在平面直角坐标系中，已知点 $\text{[math]}$ ，以原点O为位似中心，相似比为 $\text{[math]}$ ，把 $\text{[math]}$ 缩小，则点A的对应点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·诸暨期末) 两个大小不一的五边形 $\text{[math]}$ 和五边形 $\text{[math]}$ 如图所示位置，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，对应连接并延长 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 刚好交于一点 $\text{[math]}$ ，则这两个五边形的关系是（）

A . 一定相似 B . 一定不相似 C . 不一定相似 D . 不能确定

答案解析收藏纠错 + 选题
9. (2024九上·南岸期末) 如图，在直角坐标系中， $\text{[math]}$ 的三个顶点分别为 $\text{[math]}$ ，现以原点O为位似中心，在第一象限内作与 $\text{[math]}$ 的位似比为2的位似图形 $\text{[math]}$ ，则顶点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·越城期末) 如图，四边形 $\text{[math]}$ 与四边形 $\text{[math]}$ 位似，位似中心点是 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. 如图，在 $\text{[math]}$ 中，O是 $\text{[math]}$ 的中点，以点O为位似中心，作 $\text{[math]}$ 的位似图形 $\text{[math]}$ .若点A的对应点D是 $\text{[math]}$ 的重心，则 $\text{[math]}$ 与 $\text{[math]}$ 的位似比为.

答案解析收藏纠错 + 选题
12. (2021九上·柯桥月考) 在平面直角坐标系中，已知矩形OA₁B₁C₁与矩形OABC关于坐标原点O位似，且矩形OA₁B₁C₁的面积等于矩形OABC面积的4倍，若矩形OABC的顶点B的坐标为B（8，6），则B的对应点B₁的坐标为．

答案解析收藏纠错 + 选题
13. (2023·浙江模拟) 如图，△OAB与△OCD是以点O为位似中心的位似图形，位似比为1∶2，∠OCD=90°，CO=CD=2，则点B的坐标为．

答案解析收藏纠错 + 选题
14.
如图，在直角坐标系中，△ABC的各顶点坐标为A（﹣1，1），B（2，3），C（0，3）．现以坐标原点为位似中心，作△A′B′C′，使△A′B′C′与△ABC的位似比为 $\text{[math]}$ ．则点A的对应点A′的坐标为

答案解析收藏纠错 + 选题
15. (2021九上·德惠期末) 如图，在平面直角坐标系中，等边△ABC与等边△BDE是以原点为位似中心的位似图形，且相似比为 $\text{[math]}$ ，点A、B、D在x轴上，若等边△BDE的边长为6，则点C的坐标为．

答案解析收藏纠错 + 选题
16. 以下四个命题：①如果三角形一边的中点到其他两边距离相等，那么这个三角形一定是等腰三角形：②两条对角线互相垂直且相等的四边形是正方形：③一组数据2，4，6.4的方差是2；④△OAB与△OCD是以O为位似中心的位似图形，且位似比为1：4，已知∠OCD=90°，OC=CD．点A、C在第一象限．若点D坐标为（2 $\text{[math]}$ ， 0），则点A坐标为（ $\text{[math]}$ ， $\text{[math]}$ ），其中正确命题有（填正确命题的序号即可）

答案解析收藏纠错 + 选题

三、解答题

17.
如图，已知△DEO与△ABO是位似图形，△OEF与△OBC是位似图形．求证：OD•OC=OF•OA．

答案解析收藏纠错 + 选题
18.
在放映电影时，我们需要把胶片上的图片放大到银幕上，以便人们欣赏．如图，点P为放映机的光源，△ABC是胶片上面的画面，△A′B′C′为银幕上看到的画面．若胶片上图片的规格是2.5cm×2.5cm，放映的银幕规格是2m×2m，光源P与胶片的距离是20cm，则银幕应距离光源P多远时，放映的图象正好布满整个银幕？

答案解析收藏纠错 + 选题
19.
如图所示的平面图的比例尺是1：5000，根据图中所示的尺寸（单位：cm）．
（1）求围墙四边的实际长度；
（2）若墙上的四个小矩形全等，猜想四个小矩形是否是位似图形．

答案解析收藏纠错 + 选题
20.
如图，△OAB以O为位似中心放大1倍到△A′OB′，写出变化前后各顶点的坐标，并指出坐标的变化规律．

答案解析收藏纠错 + 选题
21.
如图，在平面直角坐标系中，△ABC和△A₁B₁C₁关于点E成中心对称，
（1）在图中标出点E，且点E的坐标为   ；
（2）点P（a，b）是△ABC边AB上一点，△ABC经过平移后点P的对应点P′的坐标为（a﹣6，b+2），请画出上述平移后的△A₂B₂C₂ ，此时A₂的坐标为     ， C₂的坐标为    ；
（3）若△A₁B₁C₁和△A₂B₂C₂关于点F成位似三角形，则点F的坐标为     ．

答案解析收藏纠错 + 选题
22.
如图，△ABC中，AD、BE是高．
1. （1）求证： $\text{[math]}$ ；
2. （2）连接DE，那么△CDE与△CAB是位似图形吗？
答案解析收藏纠错 + 选题
23.
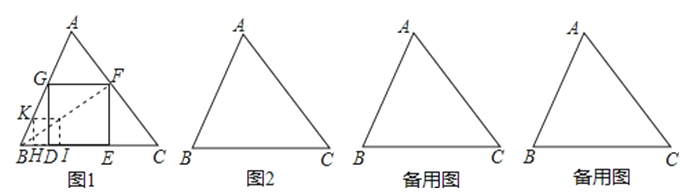
如图1，给定锐角三角形ABC，小明希望画正方形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上，他发现直接画图比较困难，于是他先画了一个正方形HIJK，是的H，I，位于射线BC上，K位于射线BA上，而不需要求J必须位于AC上．这是他发现可以将正方形HIJK通过放大或缩小得到满足要求的正方形DEFG．
阅读以上材料，回答小明接下来研究的以下问题：
（1）如图2，给定锐角三角形ABC，画出所有长宽比为2：1的长方形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上．
（2）已知三角形ABC的面积为36，BC=12，在第（1）问的条件下，求长方形DEFG的面积．

答案解析收藏纠错 + 选题