浙江省绍兴市诸暨市2022-2023学年九年级上学期期末数学...

更新时间：2023-03-21 浏览次数：186 类型：期末考试

一、选择题（本大题有10小题，每小题4分，共40分.）

1. (2023九上·诸暨期末) 已知 $\text{[math]}$ 关于 $\text{[math]}$ 的二次函数解析式为 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . ±2 B . 1 C . -2 D . ±1

答案解析收藏纠错 + 选题
2. (2023九上·诸暨期末) 小明任意抛掷一枚均匀骰子，六个面上分别刻着“1~6”的整数.抛掷一次正面朝上为偶数的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九下·婺城月考) 点 $\text{[math]}$ 到圆 $\text{[math]}$ 的距离为6，若点 $\text{[math]}$ 在圆 $\text{[math]}$ 外，则圆 $\text{[math]}$ 的半径 $\text{[math]}$ 满足（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·武义月考) 已知实数 $\text{[math]}$ 、 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 6 D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·武义月考) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九上·武义月考) 如图为一座拱形桥示意图，桥身 $\text{[math]}$ （弦 $\text{[math]}$ ）长度为8，半径 $\text{[math]}$ 垂直 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，则桥拱高 $\text{[math]}$ 为（）

A . 3 B . 2.5 C . 2 D . 1.5

答案解析收藏纠错 + 选题
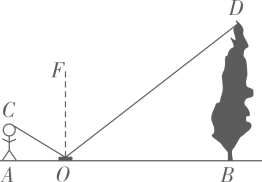
7. (2023九上·武义月考) 如图，某同学利用镜面反射的原理巧妙地测出了树的高度，已知人的站位点 $\text{[math]}$ ，镜子 $\text{[math]}$ ，树底 $\text{[math]}$ 三点在同一水平线上，眼睛与地面的高度为1.6米， $\text{[math]}$ 米， $\text{[math]}$ 米，则树高为（）米

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
8. (2023九上·诸暨期末) 要得到二次函数 $\text{[math]}$ 图象，需将 $\text{[math]}$ 的图象（）

A . 先向左平移2个单位，再向下平移2个单位 B . 先向右平移2个单位，再向上平移2个单位 C . 先向左平移1个单位，再向上平移1个单位 D . 先向右平移1个单位，再向下平移1个单位

答案解析收藏纠错 + 选题
9. (2023九上·柯桥月考) 二次函数 $\text{[math]}$ 中当 $\text{[math]}$ 时 $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大，则一次项系数 $\text{[math]}$ 满足（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·诸暨期末) 两个大小不一的五边形 $\text{[math]}$ 和五边形 $\text{[math]}$ 如图所示位置，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，对应连接并延长 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 刚好交于一点 $\text{[math]}$ ，则这两个五边形的关系是（）

A . 一定相似 B . 一定不相似 C . 不一定相似 D . 不能确定

答案解析收藏纠错 + 选题

二、填空题（本大题有6小题，每小题5分，共30分.）

11. (2023九上·诸暨期末) 已知 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2023九上·武义月考) 如图，中位线 $\text{[math]}$ 将 $\text{[math]}$ 分成面积为 $\text{[math]}$ ， $\text{[math]}$ 上下两部分 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
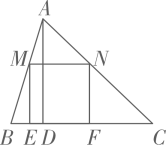
13. (2023九上·武义月考) 如图， $\text{[math]}$ 中边 $\text{[math]}$ ，高 $\text{[math]}$ ，正方形 $\text{[math]}$ 的四个顶点分别为 $\text{[math]}$ 三边上的点（点 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 上的点，点 $\text{[math]}$ 为 $\text{[math]}$ 上的点，点 $\text{[math]}$ 为 $\text{[math]}$ 上的点），则正方形 $\text{[math]}$ 的边长为.

答案解析收藏纠错 + 选题
14. (2023九上·武义月考) 如图，点 $\text{[math]}$ 为 $\text{[math]}$ 上的黄金分割点 $\text{[math]}$ ， $\text{[math]}$ ，作如下操作：
步骤1：以点 $\text{[math]}$ 为圆心，小于1为半径作圆弧，分别与 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ；

步骤2：作 $\text{[math]}$ 的中垂线 $\text{[math]}$ ；

步骤3：以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径为圆弧交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ .

则线段 $\text{[math]}$ ， $\text{[math]}$ ，圆弧 $\text{[math]}$ 围成的几何图形面积为.

答案解析收藏纠错 + 选题
15. (2023九上·诸暨期末) 如图，抛物线 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为常数，且 $\text{[math]}$ ）交 $\text{[math]}$ 轴于 $\text{[math]}$ ， $\text{[math]}$ 两点，则不等式 $\text{[math]}$ 的解为.

答案解析收藏纠错 + 选题
16. (2024九上·余杭月考) 三角形三边长为5，5，6，则这个三角形的外心 $\text{[math]}$ 和重心 $\text{[math]}$ 的距离为.

答案解析收藏纠错 + 选题

三、解答题（本大题有8小题，第17~20小题每小题8分，第21小题10分，第22，23小题每小题12分，第24小题14分，共80分.）

17. (2023九上·诸暨期末)
1. （1）计算： $\text{[math]}$ ；
2. （2）已知二次函数顶点为 $\text{[math]}$ ，经过点 $\text{[math]}$ ，求该二次函数的一般式.
答案解析收藏纠错 + 选题
18. (2023九上·诸暨期末) 如图，转盘的红色扇形和蓝色扇形的圆心角分别为 $\text{[math]}$ 和 $\text{[math]}$ ，转盘可以自由转动.
1. （1）转动一次转盘，求指针落在红色扇形内的概率；
2. （2）转动两次转盘，利用树状图或者列表法分析指针两次都落在蓝色扇形内的概率.
答案解析收藏纠错 + 选题
19. (2023九上·诸暨期末) 如图，在一片海域中有三个岛屿，标记为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .经过测量岛屿 $\text{[math]}$ 在岛屿 $\text{[math]}$ 的北偏东 $\text{[math]}$ ，岛屿 $\text{[math]}$ 在岛屿 $\text{[math]}$ 的南偏东 $\text{[math]}$ ，岛屿 $\text{[math]}$ 在岛屿 $\text{[math]}$ 的南偏东 $\text{[math]}$ .
1. （1）直接写出 $\text{[math]}$ 的三个内角度数；
2. （2）小明测得较近两个岛屿 $\text{[math]}$ ，求 $\text{[math]}$ 、 $\text{[math]}$ 的长度（最终结果保留根号，不用三角函数表示）.
答案解析收藏纠错 + 选题
20. (2023九下·婺城月考) 某水果批发商场经销一种水果，如果每千克盈利10元，每天可售出500千克.经市场调查发现，在进货价格不变的情况下，若每千克每涨价1元，日销售量将减少20千克.
1. （1）设每千克涨价为 $\text{[math]}$ 元，每天的总盈利为 $\text{[math]}$ 元.若涨价 $\text{[math]}$ 为整数，则总盈利 $\text{[math]}$ 最大值为多少？
2. （2）若商场只要求保证每天的盈利为6000元，每千克应涨价多少元？
答案解析收藏纠错 + 选题
21. (2023九上·诸暨期末) 如图，圆 $\text{[math]}$ 中延长弦 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，判断 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 满足什么数量关系时， $\text{[math]}$ ？请说明理由.
答案解析收藏纠错 + 选题
22. (2023九上·诸暨期末) 如图，菱形 $\text{[math]}$ 边长为4，对角线交于点 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 上一点， $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，取 $\text{[math]}$ 中点 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的长度；
2. （2）求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
23. (2023九上·诸暨期末) 已知函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ 为常数）的图象经过点 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ 的值；
2. （2）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的最大值与最小值之差；
3. （3）当 $\text{[math]}$ 时，若 $\text{[math]}$ 的最大值与最小值之差为8，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
24. (2023九上·诸暨期末) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 上一定点，点 $\text{[math]}$ 为 $\text{[math]}$ 上一动点， $\text{[math]}$ ， $\text{[math]}$ 两点关于 $\text{[math]}$ 的对称点为 $\text{[math]}$ ， $\text{[math]}$ .当点 $\text{[math]}$ 运动时，始终满足 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 、 $\text{[math]}$ 的长度；
2. （2）当 $\text{[math]}$ 与 $\text{[math]}$ 一边垂直时，求 $\text{[math]}$ 的长度；
3. （3）当 $\text{[math]}$ 与 $\text{[math]}$ 任意边既不垂直也不重合时，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题