浙江省新晖联盟2023年中考三模数学试题

更新时间：2023-07-25 浏览次数：156 类型：中考模拟

一、选择题（本题有10小题，每小题4分，共40分．）

1. (2023·浙江模拟) 2023的相反数是（）

A . 2023 B . $\text{[math]}$ C . -2023 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024七上·永康期中) 第19届亚运会即将在杭州举办，据官网消息杭州奥体中心体育场建筑总面积约为216000平方米，数据216000用科学记数法表示为（）

A . 2.16×10⁵ B . 21.6×10⁴ C . 2.16×10⁴ D . 216×10³

答案解析收藏纠错 + 选题
3. 如图，由5个完全相同的小正方体组合成一个立体图形，它的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023·浙江模拟) 下列运算正确的是（）

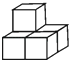
A . 4a+3b=7ab B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·浙江模拟) 亚运某志愿者小分队年龄情况如下：则这12名队员年龄的众数、中位数分别是（）
年龄（岁）
19
20
21
22
23
人数（名）
2
5
2
2
1

A . 2名，20岁 B . 5名，20岁 C . 20岁，20岁 D . 20岁，20.5岁

答案解析收藏纠错 + 选题
6. (2023·浙江模拟) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，根据尺规作图的痕迹判断以下结论错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023·浙江模拟) 已知圆锥的底面半径为5cm，高线长为12cm，则圆锥的侧面积为（）cm²

A . 130π B . 120π C . 65π D . 60π

答案解析收藏纠错 + 选题
8. (2023·浙江模拟) 《九章算术》是我国东汉初年编订的一部数学经典著作，在它的“方程”一章里，一次方程组是由算筹布置而成的．《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图1、图2．图中各行从左到右列出的算筹数分别表示未知数x，y的系数与相应的常数项，把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是 $\text{[math]}$ ，类似地，图2所示的算筹图我们可以表述为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·浙江模拟) 已知点（x₁ ， y₁），（x₂ ， y₂）为二次函数y=-x²图象上的两点（不为顶点），则以下判断正确的是（）

A . 若x₁>x₂ ，则y₁>y₂ B . 若x₁<x₂ ，则y₁<y₂ C . 若： $\text{[math]}$ ，则y₁>y₂ D . 若 $\text{[math]}$ ，则y₁<y₂

答案解析收藏纠错 + 选题
10. 如图，在Rt△ABC中，∠C=90°，BC=4， $\text{[math]}$ ． ⊙C的半径长为2，P是△ABC边上一动点（可以与顶点重合），并且点P到⊙C的切线长为m．若满足条件的点P有4个，则m的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题有6小题，每小题5分，共30分）

11. (2023·浙江模拟) 分解因式：x³-4x= ．

答案解析收藏纠错 + 选题
12. (2023·浙江模拟) 即将举行的杭州亚运会吉祥物“宸宸”、“琼琼”、“莲莲”，将三张正面分别印有以上3个吉祥物图案的卡片（卡片的形状、大小、质地都相同）背面朝上、洗匀，若先从中任意抽取1张，记录后放回，洗匀，再从中任意抽取1张，两次抽取的卡片图案相同的概率是．

答案解析收藏纠错 + 选题
13. (2023·浙江模拟) 如图，△OAB与△OCD是以点O为位似中心的位似图形，位似比为1∶2，∠OCD=90°，CO=CD=2，则点B的坐标为．

答案解析收藏纠错 + 选题
14. (2023·浙江模拟) 在平面直角坐标系xOy中，给出如下定义：点A到x轴、y轴距离的较大值，称为点A的“长距”，当点P的“长距”等于点Q的“长距”时，称P，Q两点为“等距点”，若P（-1，4），Q（k+3，4k-3）两点为“等距点”，则k的值为．

答案解析收藏纠错 + 选题
15. (2023八下·仪征期末) 如图， $\text{[math]}$ 位于平面直角坐标系中，点B在x轴正半轴上，点A及 $\text{[math]}$ 的中点D在反比例函数 $\text{[math]}$ 的图象上，点C在反比例函数 $\text{[math]}$ 的图象上，则k的值为.

答案解析收藏纠错 + 选题
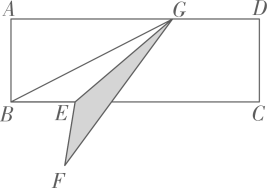
16. (2023·浙江模拟) 如图，在矩形ABCD中，点G在AD上，且GD=AB=1，AG=3，点E是线段BC上的一个动点（点E不与点B，C重合），连接GB，GE，将△GBE关于直线GE对称的三角形记作△GFE，当点E运动到使点F落在矩形任意一边所在的直线上时，则线段BE的长是．

答案解析收藏纠错 + 选题

三、解答题（本题有8小题，第17~20小题每小题8分，第21小题10分，第22，23小题每小题12分，第24小题14分，共80分．解答需写出必要的文字说明、演算步骤或证明过程）

17. (2023·浙江模拟) 化简与计算
1. （1）化简：（x+1）²-x（x+1）
2. （2）计算： $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2023·浙江模拟) 杭州第19届亚运会，绍兴市将承办篮球、排球、棒球、垒球、攀岩5个项目的比赛，为了解学生对这些比赛项目的喜欢程度，某校随机抽查了部分学生进行问卷调查，要求每名学生只选其中最喜欢的一个项目，并将抽查结果绘制成如图不完整的统计图。
根据图中信息，解答下列问题：
1. （1）本次接受问卷调查的学生有多少人？
2. （2）在图1中补全条形统计图，并求图2中“攀岩”的扇形圆心角的度数。
3. （3）全校共有1500名学生，请你估计全校学生中最喜欢“排球”的学生有多少人．
答案解析收藏纠错 + 选题
19. (2023·浙江模拟) 大善塔位于绍兴市区城市广场东南角，始建于梁天监三年（504），为明代建筑，在一次数学综合实践活动中，李老师布置了一个任务：请根据所学知识设计一种方案，测量大善塔的高。
1. （1）【实践探究】某小组通过思考，绘制了如图2所示的测量示意图，即在水平地面上的点C处测得塔顶端A的仰角为 $\text{[math]}$ ，点C到点B的距离BC=a米，即可得出塔高AB=米（请你用 $\text{[math]}$ 和a表示）．
2. （2）【问题解决】但在实践中发现：由于无法直接到达塔底端的B点，因此BC无法直接测量，该小组对测量方案进行了如下修改：如图3，从水平地面的C点向前走到点D处，在D处测得塔顶端A的仰角为 $\text{[math]}$ ，即可通过计算求得塔高AB，若测得的 $\text{[math]}$ ， $\text{[math]}$ ， CD=26米，请你利用所测数据计算塔高AB．（计算结果精确到0.1米，参考数据： $\text{[math]}$ ）
答案解析收藏纠错 + 选题
20. (2023·浙江模拟) 绍兴首条智慧快速路于今年3月19日正式通车，该快速路上M，N两站相距20km，甲、乙两名杭州亚运会会务工作志愿者从M站出发前往N站附近的比赛场馆开展服务，甲乘坐无人驾驶小巴，乙乘坐无人驾驶汽车，甲比乙提前5分钟出发，图中OC，AB分别表示甲、乙离开M站的路程s（km）与时间t（min）的函数关系的图象。
根据图象解答下列问题：
1. （1）求乙离开M站的路程s（km）与时间t（min）的函数关系式．
2. （2）在两车都行驶的过程中，当汽车与小巴相距2千米时，求t的值．
答案解析收藏纠错 + 选题
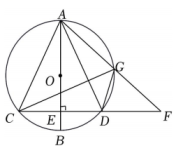
21. (2023·浙江模拟) 如图，AB为⊙O的直径，弦CD⊥AB于点E，G为劣弧AD上一动点，AG与CD的延长线交于点F，连接AC、AD、CG、DG．记tan∠DGF=m（m为常数，且m>1）．
1. （1）求证：∠AGC=∠ACF；
2. （2）求 $\text{[math]}$ 的值（用含m的式子表示）．
答案解析收藏纠错 + 选题
22. (2023·浙江模拟) 在△ABC中，CD平分∠ACB交AB于点D，点E是射线AB上的动点（不与点D重合），过点E作 $\text{[math]}$ 交直线CD于点F，∠BEF的角平分线所在的直线与射线CD交于点G．
1. （1）如图1，点E在线段AD上运动．
  ①若∠B=60°，∠ACB=40°则∠EGC= ▲ °；
  ②若∠A=90°，求∠EGC的度数；
2. （2）若点E在射线DB上运动时，探究∠EGC与∠A之间的数量关系．
答案解析收藏纠错 + 选题
23. (2023·浙江模拟) 已知抛物线y=x²+bx+c的对称轴为直线x=2．
1. （1）求b的值：
2. （2）当1≤x≤4时，函数值y的最大值与最小值的和为6，求c的值：
3. （3）当1<x<4时，抛物线与x轴有且只有一个交点，求c的取值范围．
答案解析收藏纠错 + 选题
24. (2023·浙江模拟) 如图
1. （1）【特殊发现】
  如图1，正方形BEFG与正方形ABCD的顶点B重合，BE、BG分别在BC、BA边上，则有：
  ① $\text{[math]}$ ；②直线DF与直线AG所夹的锐角等于度；
2. （2）【类比探究】
  将图1中的正方形BEFG绕点B逆时针旋转，连接DF、AG，如图2，则（1）中的结论是否成立，请说明理由；
3. （3）【解决问题】
  如图3，点P是正方形ABCD的AB边上一动点（不与A、B重合），连接PC，沿PC将△PBC翻折到△PEC位置，连接DE并延长，与CP的延长线交于点F，连接AF，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题