一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1.
(2023八上·孟村期中)
如果热量用Q表示,电流用I表示,电阻用R表示,时间用/表示,则焦耳定律为

, 则下列特殊字体下的字母是轴对称图形的是( )
-
-
-
A . 正六边形
B . 正三角形
C . 六边形
D . 不能确定
-
-
6.
(2023八上·孟村期中)
邢台主城区持续打造“五分钟健身圈”,2023年底前将再建40家健身驿站,总数达到100家.如图,有三个小区的位置成三角形,现决定在三个小区之间修建一个健身驿站,使该驿站到三个小区的距离相等,则驿站应建在( )

A . 三条中线的交点处
B . 三条角平分线的交点处
C . 三条高线的交点处
D . 三条边的垂直平分线的交点处
-
-
A .  的长度不能随意取
B .
的长度不能随意取
B .  的长度也是任意长度
C .
的长度也是任意长度
C .  的长度是任意长度
D .
的长度是任意长度
D .  的长度必须等于
的长度必须等于
-
A . 锐角三角形
B . 直角三角形
C . 钝角三角形
D . 不能确定
-
-
A . 30°
B . 45°
C . 60°
D . 条件不足,无法计算
-
12.
(2023八上·孟村期中)
下面是雨伞在开合过程中某时刻的截面图,伞骨

, 点D、E分别是

、

的中点,

、

是连接弹簧和伞骨的支架,且

, 则判定“

”的依据是( )

A . 角边角
B . 角角边
C . 边边边
D . 边边角
-
A . 120°
B . 110°
C . 80°
D . 100°
-
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
-
15.
(2023八上·孟村期中)
如图,在

中,点D在边

上,

,

,

, 垂足分别为E,F,

.

求证: .以下是排乱的证明过程:
.以下是排乱的证明过程:
证明过程正确的顺序是( )
A . ④→②→③→①
B . ④→③→①→②
C . ③→②→①→④
D . ③→①→④→②
-
16.
(2023八上·孟村期中)
对于试题“在

中,

, 过点A作

, 求使

恰好把

分成两个等腰三角形时的条件”,甲乙丙三人的说法如下:
甲: ;乙:
;乙: ,
,  ;丙:
;丙: .
.
下面说法正确的是( )
A . 甲说法正确
B . 甲、乙说法正确
C . 甲、乙、丙说法都正确
D . 三种说法都正确但不全面
二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分.把答案写在题中横线上)
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
20.
(2023八上·孟村期中)
下面是多媒体上的一道习题:
请将下面的解题过程补充完整。
解:延长 至点E,使 至点E,使 , 连接 , 连接 . . ∵ 是 是 的中线, 的中线, ∴ ▲ . ▲ . 在 和 和 中, 中, ∴ (填判定定理用字母表示) (填判定定理用字母表示) ∴ ▲ , ▲ , 在 中,根据“三角形三边关系”可知 中,根据“三角形三边关系”可知 ∴ ▲  ▲ ▲ 又 ∴ ▲  ▲ ▲ 
|
-
-
-
(2)
点B坐标是
,点

坐标是
;
-
(3)
求

的面积.
-
-
(1)
用尺规作

边的垂直平分线;(保留作图痕迹,不写作法)
-
(2)

边的垂直平分线分别交

、

于点D、E,连接

, 若

的周长是10,求

.
-
-
24.
(2023八上·孟村期中)
廊坊某初中数学兴趣小组为测量路灯高度,设计了如下方案,请据此求出路灯高度

.
主题 | 测量路灯高度 |
工具 | 测角仪、皮尺等 |
人员 | 组长:xxx;组员:xxx、xxx、xxx |
示意图 | 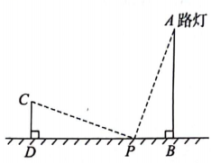
|
方案 | 在路灯前选一点P,并测出 , 然后把说明竖直竹竿 , 然后把说明竖直竹竿 在 在 的延长线上左右移动到某处, 的延长线上左右移动到某处, 地面, 地面, 地面处,并测出 地面处,并测出 . . |
数据 |  , ,  , ,  , ,  , , 
|
评价 | |
-
-
(1)
当

, 则

度;
-
(2)
当

, 则

度;
-
(3)
当

, 则

度;
-
(4)
请写出

与
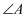
的数量关系,并证明.
-
-
(1)
点E能否是

中点?
(填“能”或“不能”)
-
(2)
求点E到直线

的距离;
-
(3)
连接

, 若

平分
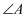
, 求

的度数.(注:等腰三角形两个底角相等)
 B .
B .  C .
C .  D .
D . 

