2013年全国高考理数真题试卷（新课标Ⅰ卷）

更新时间：2021-05-20 浏览次数：1321 类型：高考真卷

一、选择题：在每小题给出的四个选项中，只有一个是符合题目要求的.

1. (2013·新课标Ⅰ卷理) 已知集合A={x|x²﹣2x＞0}， $\text{[math]}$ ，则（）

A . A∩B=∅ B . A∪B=R C . B⊆A D . A⊆B

答案解析收藏纠错 + 选题
2. (2013·新课标Ⅰ卷理) 若复数z满足（3﹣4i）z=|4+3i|，则z的虚部为（）

A . ﹣4 B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2013·新课标Ⅰ卷理) 为了解某地区中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是（）

A . 简单的随机抽样 B . 按性别分层抽样 C . 按学段分层抽样 D . 系统抽样

答案解析收藏纠错 + 选题
4. (2013·新课标Ⅰ卷理) 已知双曲线C： $\text{[math]}$ （a＞0，b＞0）的离心率为 $\text{[math]}$ ，则C的渐近线方程为（）

A . y= $\text{[math]}$ B . y= $\text{[math]}$ C . y=±x D . y= $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2013·新课标Ⅰ卷理) 执行程序框图，如果输入的t∈[﹣1，3]，则输出的s属于（）

A . [﹣3，4] B . [﹣5，2] C . [﹣4，3] D . [﹣2，5]

答案解析收藏纠错 + 选题
6. (2013·新课标Ⅰ卷理)
如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6cm，如不计容器的厚度，则球的体积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2013·新课标Ⅰ卷理) 设等差数列{a_n}的前n项和为S_n ，若S_m_﹣₁=﹣2，S_m=0，S_m+1=3，则m=（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
8. (2013·新课标Ⅰ卷理) 某几何体的三视图如图所示，则该几何体的体积为（）

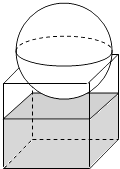
A . 16+8π B . 8+8π C . 16+16π D . 8+16π

答案解析收藏纠错 + 选题
9. (2020高二下·肥城期中) 设m为正整数，（x+y）^2m展开式的二项式系数的最大值为a，（x+y）^2m+1展开式的二项式系数的最大值为b，若13a=7b，则m=（）

A . 5 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题
10. (2013·新课标Ⅰ卷理) 已知椭圆E： $\text{[math]}$ 的右焦点为F（3，0），过点F的直线交椭圆E于A、B两点．若AB的中点坐标为（1，﹣1），则E的方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2013·新课标Ⅰ卷理) 已知函数f（x）= $\text{[math]}$ ，若|f（x）|≥ax，则a的取值范围是（）

A . （﹣∞，0] B . （﹣∞，1] C . [﹣2，1] D . [﹣2，0]

答案解析收藏纠错 + 选题
12. (2013·新课标Ⅰ卷理) 设△A_nB_nC_n的三边长分别为a_n ， b_n ， c_n ， △A_nB_nC_n的面积为S_n ， n=1，2，3…若b₁＞c₁ ， b₁+c₁=2a₁ ， a_n+1=a_n ， $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . {S_n}为递减数列 B . {S_n}为递增数列 C . {S_2n_﹣₁}为递增数列，{S_2n}为递减数列 D . {S_2n_﹣₁}为递减数列，{S_2n}为递增数列

答案解析收藏纠错 + 选题

二、填空题

13. (2013·新课标Ⅰ卷理) 已知两个单位向量 $\text{[math]}$ ， $\text{[math]}$ 的夹角为60°， $\text{[math]}$ =t $\text{[math]}$ +（1﹣t） $\text{[math]}$ ．若 $\text{[math]}$ • $\text{[math]}$ =0，则t=．

答案解析收藏纠错 + 选题
14. (2020高二上·番禺期末) 若数列{a_n}的前n项和为S_n= $\text{[math]}$ a_n+ $\text{[math]}$ ，则数列{a_n}的通项公式是a_n=．

答案解析收藏纠错 + 选题
15. (2013·新课标Ⅰ卷理) 设当x=θ时，函数f（x）=sinx﹣2cosx取得最大值，则cosθ=．

答案解析收藏纠错 + 选题
16. (2013·新课标Ⅰ卷理) 若函数f（x）=（1﹣x²）（x²+ax+b）的图象关于直线x=﹣2对称，则f（x）的最大值为．

答案解析收藏纠错 + 选题

三、解答题：解答应写出文字说明，证明过程或演算步骤.

17. (2023高二上·福州期中) 如图，在△ABC中，∠ABC=90°， $\text{[math]}$ ，BC=1，P为△ABC内一点，∠BPC=90°
1. （1）若 $\text{[math]}$ ，求PA；
2. （2）若∠APB=150°，求tan∠PBA．
答案解析收藏纠错 + 选题
18. (2013·新课标Ⅰ卷理) 如图，三棱柱ABC﹣A₁B₁C₁中，CA=CB，AB=AA₁ ， ∠BAA₁=60°．
1. （1）证明AB⊥A₁C；
2. （2）若平面ABC⊥平面AA₁B₁B，AB=CB，求直线A₁C与平面BB₁C₁C所成角的正弦值．
答案解析收藏纠错 + 选题
19. (2013·新课标Ⅰ卷理) 一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n．如果n=3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果n=4，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．假设这批产品的优质品率为50%，即取出的产品是优质品的概率都为 $\text{[math]}$ ，且各件产品是否为优质品相互独立．
1. （1）求这批产品通过检验的概率；
2. （2）已知每件产品检验费用为100元，凡抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X（单位：元），求X的分布列及数学期望．
答案解析收藏纠错 + 选题
20. (2013·新课标Ⅰ卷理) 已知圆M：（x+1）²+y²=1，圆N：（x﹣1）²+y²=9，动圆P与圆M外切并与圆N内切，圆心P的轨迹为曲线C．
1. （1）求C的方程；
2. （2） l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P的半径最长时，求|AB|．
答案解析收藏纠错 + 选题
21. (2013·新课标Ⅰ卷理) 已知函数f（x）=x²+ax+b，g（x）=e^x（cx+d）若曲线y=f（x）和曲线y=g（x）都过点P（0，2），且在点P处有相同的切线y=4x+2．
1. （1）求a，b，c，d的值；
2. （2）若x≥﹣2时，f（x）≤kg（x），求k的取值范围．
答案解析收藏纠错 + 选题

四、请考生在第22、23、24题中任选一道作答，并用2B铅笔将答题卡上所选的题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分，不涂，按本选考题的首题进行评分.

22. (2013·新课标Ⅰ卷理) 如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D．
1. （1）证明：DB=DC；
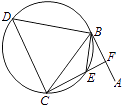
2. （2）设圆的半径为1，BC= $\text{[math]}$ ，延长CE交AB于点F，求△BCF外接圆的半径．
答案解析收藏纠错 + 选题
23. (2013·新课标Ⅰ卷理) （选修4﹣4：坐标系与参数方程）
已知曲线C₁的参数方程为 $\text{[math]}$ （t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C₂的极坐标方程为ρ=2sinθ．
1. （1）把C₁的参数方程化为极坐标方程；
2. （2）求C₁与C₂交点的极坐标（ρ≥0，0≤θ＜2π）
答案解析收藏纠错 + 选题
24. (2013·新课标Ⅰ卷理) 已知函数f（x）=|2x﹣1|+|2x+a|，g（x）=x+3．
1. （1）当a=﹣2时，求不等式f（x）＜g（x）的解集；
2. （2）设a＞﹣1，且当 $\text{[math]}$ 时，f（x）≤g（x），求a的取值范围．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2013年全国高考理数真题试卷（新课标Ⅰ卷）

副标题：

*注意事项：

2013年全国高考理数真题试卷（新课标Ⅰ卷）

试题分析

总体分析

题量分析

难度分析

知识点分析