一、选择题(12小题,每小题3分,共36分,每小题给出的四个选项中只有一项是正确)
-
A . 3cm , 5cm , 10cm
B . 5cm , 4cm , 8cm
C . 2cm , 4cm , 6cm
D . 3cm , 3cm , 7cm
-
2.
若分式

有意义,则
x的取值范围是( )
A . x≠-1
B . x≠0
C . x≠1
D . x≠2
-
A . 两点之间线段最短
B . 三角形具有稳定性
C . 经过两点有且只有一条直线
D . 垂线段最短
-
4.
(2023八上·桂平期中)
PM2.5是指大气中直径小于或等于2.5μ
m(1μ
m=0.000001
m)的颗粒物,也称为可入肺颗粒物,它们含有一定量的有毒、有害物质,对人体健康和大气环境质量有很大影响,2.5μ
m用科学记数法可表示为( )
A . 25×10-5m
B . 2.5×10-5m
C . 2.5×10-6m
D . 0.25×10-7m
-
A . a+a2=a3
B . a•a2=a3
C . a6÷a2=a3
D . (a-1)3=a3
-
6.
(2023八上·桂平期中)
在测量一个小口圆形容器的壁厚时,小明用“
X型转动钳”按如图方法进行测量,其中
OA=
OD ,
OB=
OC , 测得
AB=5厘米,
EF=6厘米,圆形容器的壁厚是( )

A . 5厘米
B . 6厘米
C . 1厘米
D .  厘米
厘米
-
A . x+2=1
B . x+2(x﹣2)=1
C . x+2(x﹣2)=﹣1
D . x+2=﹣1
-
A . 三个角都是  的三角形是等边三角形
B . 两个锐角的和是钝角
C . 若
的三角形是等边三角形
B . 两个锐角的和是钝角
C . 若  ,则
,则  D . 在同一平面内,若直线
D . 在同一平面内,若直线  ,
,  ,则
,则 
-
9.
(2023八上·桂平期中)
一艘轮船在两个码头之间航行,顺水航行81
km所需的时间与逆水航行69
km所需的时间相同.已知水流速度是速度2
km/
h , 则轮船在静水中航行的速度是( )
A . 25km/h
B . 24km/h
C . 23km/h
D . 22km/h
-
A . 1
B . 0
C . ﹣4
D . ﹣5
-
11.
(2023八上·桂平期中)
如图,△
ABC中,点
D ,
E分别在∠
ABC和∠
ACB的平分线上,连接
BD ,
DE ,
EC , 若∠
D+∠
E=295°,则∠
A等于( )

A . 65°
B . 60°
C . 55°
D . 50°
-
12.
(2023八上·桂平期中)
如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )

A . 7.5
B . 5
C . 4
D . 不能确定
二、填空题(本大题共6小题,每小题2分,共12分,)
-
-
-
15.
(2023八上·桂平期中)
如图,已知△
ABC≌△
ADE ,
D是∠
BAC平分线上一点,∠
BAC=76.6°,则∠
CAE=
°.

-
-
17.
(2023八上·桂平期中)
如图,将直角三角形纸片ABC进行折叠,使直角顶点A落在斜边BC上的点E处,并使折痕经过点C,得到折痕CD.若∠CDE=70°,则∠B=
°.

-
18.
(2023八上·桂平期中)
如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第100个图形中等边三角形的个数是
.

三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
-
-
-
21.
综合与实践
-
(1)
问题探究:如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在

和

上分别取点C和D,使得

, 连接

, 以

为边作等边三角形

, 则

就是

的平分线.

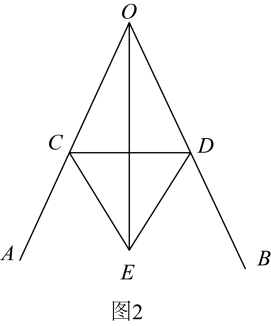
请写出 平分
平分 的依据:;
的依据:;
-
-
(3)
拓展实践:

小明将研究应用于实践.如图4,校园的两条小路 和
和 , 汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
, 汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
-
22.
(2023八上·桂平期中)
下面是小明同学进行分式化简的过程,请认真阅读并完成相应任务.
 ,
,
= …第一步,
…第一步,
= …第二步,
…第二步,
= …第三步,
…第三步,
= …第四步,
…第四步,
= …第五步,
…第五步,
= …第六步.
…第六步.
-
(1)
任务一:填空:
①以上化简步骤中,第 步是进行分式的通分,通分的依据是 或填为:;
②第 步开始出现错误,这一步错误的原因是 ;
-
(2)
任务二:请直接写出该分式化简后的正确结果是 ;
-
(3)
任务三:根据小明同学进行分式化简的过程:完成下列分式的计算:

.
-
23.
(2023八上·桂平期中)
如图,△
ABC为等边三角形,
DE∥
AC , 点
O为线段
BC上一点,
DO的延长线与
AC的延长线交于点
F ,
DO=
FO .

-
-
-
24.
(2023八上·桂平期中)
为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买
A种图书花费了3000元,购买
B种图书花费了1600元,
A种图书的单价是
B种图书的1.5倍,购买
A种图书的数量比
B种图书多20本.
-
-
(2)
书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了A种图书20本和B种图书25本,共花费多少元?
-
-
-
(1)
某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在

中,

,

, 直线l经过点A,

直线l,

直线l,垂足分别为点D、E.证明:

.
-
(2)
组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在

中,

, D、A、E三点都在直线l上,并且有

, 其中α为任意锐角或钝角.请问结论

是否成立?如成立,请你给出证明;若不成立,请说明理由.
-
(3)
数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过

的边

向外作正方形

和正方形

,

是

边上的高,延长

交

于点I,求证:I是

的中点.






平分
的依据:;

不一定必须是等边三角形,只需
即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在
的边
,
上分别取
, 移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线
是
的平分线,请说明此做法的理由;

和
, 汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
