


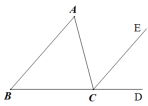





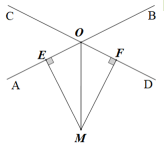

如图,某地有两个小区A,B和两条相交的供水管道OC,OD.现计划在S区域内修建一个蓄水池,要求到两个小区的距离相等,到两条公路的距离也相等,请确定蓄水池的位置.(保留作图痕迹,不写作法)

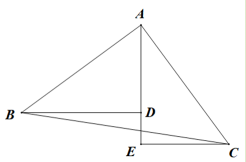

⑴将△ABC向左平移4个单位长度得到△ , 请作出△
;
⑵请作出△ABC关于轴对称的△
;
⑶请写出点 ,
的坐标.
供选择的条件:①AB=DE;②∠ACB=∠DFE;③∠A=∠D.

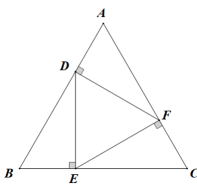

三角形的内角和定理:三角形的内角和等于180°.

已知:如图,△ABC
求证:∠A+∠B+∠C=180°
证明:在BC上任取一点D,过点D作DE∥AB,交AC于点E,过点D作DF∥AC,交AB于点F.
如图1,在等腰直角△ABC中,∠B=90°,AB=BC,将△ABD沿着AD折叠得到△AED,AB的对应边AE落在AC上,点B的对应点为E,折痕AD交BC于点D.
求证:AC=AB+BD;
如图2,AD是△ABC的角平分线,∠C=2∠B.求证:AB=AC+DC;

如图3,在△ABC中,∠ABC=2∠C,AD是△ABC的外角的平分线,交CB的延长线于点D.请你直接写出线段AC,AB,BD之间的数量关系.
