一、单项选择题(本大题6小题,每小题3分,共18分)
-
-
A . 2,5,8
B . 3,4,5
C . 5,5,10
D . 1,6,7
-
-
A . 1
B . 1.5
C . 2
D . 4
-
5.
(2023八上·章贡期中)
如图,已知

.下面是“作一个角等于已知角,即作

”的尺规作图痕迹.该尺规作图中两三角形全等的依据是( )
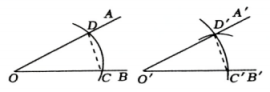
A . SAS
B . SSS
C . AAS
D . ASA
-
6.
(2023八上·章贡期中)
如图,
C为线段
AE上一动点(不与点
A ,
E重合),在
AE同侧分别作正三角形
ABC和正三角形
CDE , 连接
AD与
BE交于点
O ,
AD与
BC交于点
P ,
BE与
CD交于点
Q , 连接
PQ.以下四个结论:①

;②

;③

;④

.其中正确的结论个数是( )

A . 1个
B . 2个
C . 3个
D . 4个
二、填空题(本大题6小题,每小题3分,共18分)
-
-
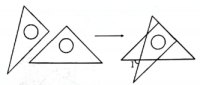
8.
(2023八上·章贡期中)
如图,一块三角形玻璃板破裂成①,②,③三块,现需要买同样大小的另一块三角形玻璃,为了方便,只需带其中一块去就行,则应带第
块碎片.(填序号)

-
-
10.
(2023八上·章贡期中)
将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则

度.
-
-
三、解答题(本大题共5小题,每小题6分,共30分)
-
-
(1)
一个多边形的内角和是它的外角和的3倍,求这个多边形的边数.
-
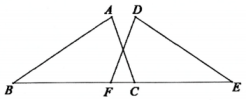
(2)
如图,

, 点
B、
F、
C、
E在同一条直线上,若

,

, 求
BF的长.
-
-
-
-
(1)
求证:

是等腰三角形:
-
-
四、解答题(本大题共3小题,每小题8分,共24分)
-
18.
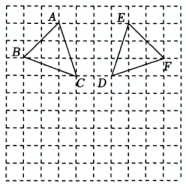
(2024八上·安陆期末)
如图所示的正方形网格中,每个小正方形的边长都为1,

,

的顶点都在网格线的交点上,在图中建立平面直角坐标系

, 使

与

关于
y轴对称,点
B的坐标为

.
-
(1)
在图中画出平面直角坐标系

;
-
(2)
①写出点
B关于
x轴的对称点

的坐标;
②画出 关于x轴对称的图形
关于x轴对称的图形 , 其中点A的对称点是
, 其中点A的对称点是 , 点C的对称点是
, 点C的对称点是 .
.
-
-
(1)
求证:

;
-
(2)
求证:

.
-
-
(1)
求证:

;
-
(2)
以
AC为边,作等边三角形

, 且点
D在
AC的左侧,连接
CD ,
AD ,
BD.求

的面积.
五、解答题(本大题共2小题,每小题9分,共18分)
-
21.
(2023八上·章贡期中)
我们定义:如图1,在四边形
ABCD中,如果

,

, 对角线
BD平分
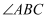
, 我们称这种四边形为“分角对补四边形”.
图1 
图2
图3
-
(1)
特例感知:如图1,在“分角对补四边形”
ABCD中,当

时,根据教材中一个重要性质直接可得

, 这个性质是
;(填序号)
①垂线段最短:②垂直平分线的性质;③角平分线的性质;④三角形内角和定理
-
(2)
猜想论证:如图2,当

为任意角时,猜想
DA与
DC的数量关系,并给予证明;
-
(3)
探究应用:如图3,在等腰

中,

,
BD平分
,
求证: .
.
-
-
(1)
若直线
CD经过

的内部,且
E ,
F在射线
CD上.
①如图1,当 时,证明:
时,证明: .
.
②如图2,若 , 当
, 当 与
与 满足什么数量关系时,①中的结论仍然成立,并说明理由.
满足什么数量关系时,①中的结论仍然成立,并说明理由.
-
(2)
如图3,若直线
CD经过

的外部,

, 猜想
EF ,
BE ,
AF三条线段的数量关系,并证明.
六、解答题(本大题共12分)
-
23.
(2023八上·章贡期中)
【课本再现】我们知道:三角形三个内角的和等于180°,利用它我们可以推出结论:
三角形的外角等于与它不相邻的两个内角的和.
图1 图2
图2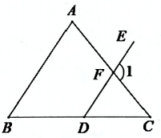 图3
图3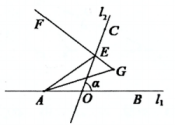
-
(1)
【定理证明】
为证明此定理,小红同学画好了图形(如图1),写好了“已知”和“求证”,请你完成证明过程,
已知:如图1, 是
是 的个外角.
的个外角.
求证: .
.
-
(2)
【知识应用】
如图2,在

中,

, 点
D在
BC边上,

交
AC于点
F , 
, 求

的度数.
-
(3)
如图3,直线

与直线

相交于点
O , 夹角

为锐角,点
B在直线

上且在点
O右侧,点
C在直线

上且在直线

上方,点
A在直线

上且在点
O左侧运动,点
E在射线
CO上运动(不与点
C、
O重合).当

时,
EF平分

,
AG平分

交直线
EF于点
G , 求

的度数,
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 



关于x轴对称的图形
, 其中点A的对称点是
, 点C的对称点是
.
.
时,证明:
.
, 当
与
满足什么数量关系时,①中的结论仍然成立,并说明理由.
是
的个外角.
.