19.
(2023高一上·成都月考)
杭州亚运会田径比赛于2023年10月5日收官.在最后两个竞技项目男女马拉松比赛中,中国选手何杰以2小时13分02秒夺得男子组冠军,这是中国队亚运史上首枚男子马拉松金牌.人类长跑运动一般分为两个阶段,第一阶段为前1小时的稳定阶段,第二阶段为疲劳阶段.现一60kg的复健马拉松运动员进行4小时长跑训练,假设其稳定阶段作速度为

的匀速运动,该阶段每千克体重消耗体力

(

表示该阶段所用时间).疲劳阶段由于体力消耗过大变为

的减速运动(

表示该阶段所用时间),疲劳阶段速度降低,体力得到一定恢复,该阶段每千克体重消耗体力

. 已知该运动员初始体力为

, 不考虑其他因素,所用时间为

(单位:h),请回答下列问题:

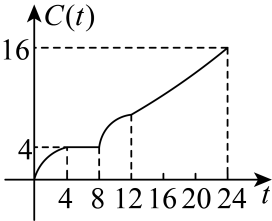 B .
B . 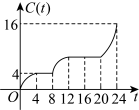 C .
C .  D .
D . 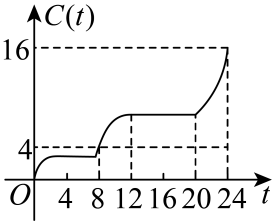
;
可得
;
可得
;
可得
.