 B .
B .  C .
C .  D .
D . 
 B .
B . 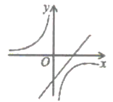 C .
C .  D .
D . 

设矩形相邻两边的长分别为 , 由矩形的面积为4,得
, 即
;由周长为
, 得
, 即
. 满足要求的
应是两个函数图象在第象限内的交点的坐标.
函数的图像如图所示,而函数
的图像可由直线
平移得到.请在同一直角坐标系中直接画出直线
.
当直线平移到与函数的图像有唯一交点
时,写出周长
的值;
若能生产出面积为4的矩形模具,求出周长的取值范围.(直接写出结论)

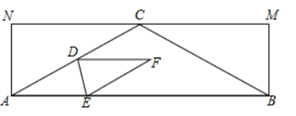
小吴发现,过点作
, 交
的延长线于点
, 通过构造
, 经过推理和计算能够使问题得到解决(如图2).