浙江省金华市婺城区2022-2023学年七年级上学期数学学业...

更新时间：2024-03-02 浏览次数：26 类型：期末考试

一、选择题(本大题有10个小题，每小题3分，共30分)

1. (2023七上·婺城期末) －2023的相反数是（）

A . 2023 B . －2023 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023七上·婺城期末) 金华市体育中心总用地面积266700平方米，总投资74200万元．其中数据266700用科学记数法表示为（）

A . 26.67×10⁴ B . 0.2667×10⁶ C . 2.667×10⁴ D . 2.667×10⁵

答案解析收藏纠错 + 选题
3. (2023七上·婺城期末) 手机移动支付给生活带来便捷．如图所示为张老师2022年12月26日移动支付账单的收支明细(正数表示收入，负数表示支出，单位：元)，张老师当天收支的最终结果是（）

A . 收入19.00元 B . 支出10元 C . 支出3.00元 D . 支出22.00元

答案解析收藏纠错 + 选题
4. (2023七上·婺城期末) 下列运算中，正确的是（）

A . a＋2a²＝3a³ B . 2a＋b＝2ab C . 4a－a＝3 D . 3ab－ab＝2ab

答案解析收藏纠错 + 选题
5. (2023七上·婺城期末) 如图，直线AB与直线CD相交于点O ，若∠AOC增大40°，则∠BOD的度数为（）

A . 减少40° B . 增大40° C . 不变 D . 增大140°

答案解析收藏纠错 + 选题
6. (2023七上·婺城期末) 在实数－2.3， $\text{[math]}$ ， 0， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，有理数的个数为a ，无理数的个数为b ，则a－b的值是（）

A . 1 B . 3 C . 2 D . 5

答案解析收藏纠错 + 选题
7. (2023七上·婺城期末) 用边长为1的正方形做了一套七巧板，拼成如图所示的一座“桥”，则“桥”中阴影部分的面积是原正方形面积的（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 不能确定

答案解析收藏纠错 + 选题
8. (2023七上·婺城期末) 我国古代数学著作《增删算法统宗》记载了“绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托．”其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x尺．则符合题意的方程是（）

A . $\text{[math]}$ x＝(x＋5)＋5 B . $\text{[math]}$ x＝(x－5)－5 C . 2x＝(x－5)－5 D . 2x＝(x＋5)＋5

答案解析收藏纠错 + 选题
9. (2023七上·婺城期末) 杭衢高铁线上，要保证衢州、金华、义乌、诸暨、杭州每两个城市之间都有高铁可乘，需要印制不同的高铁票（）

A . 20种 B . 15种 C . 10种 D . 5种

答案解析收藏纠错 + 选题
10. (2023七上·婺城期末) 在数轴上有间隔相等的四个点M ， N ， P ， Q ，所表示的数分别为m ， n ， p ， q ，其中有两个数互为相反数，若m的绝对值最大，则数轴的原点是（）

A . 点N B . 点P C . 点P或NP的中点 D . 点P或PQ的中点

答案解析收藏纠错 + 选题

二、填空题(本大题有6个小题，每小题4分，共24分)

11. (2023七上·婺城期末) 如果向东走3km记作 $\text{[math]}$ ，那么向西走4km记作km.

答案解析收藏纠错 + 选题
12. (2024九上·诸暨月考) 如图所示为同一时刻莫斯科与北京的时间，则当莫斯科时间为17：08时，北京时间为．
莫斯科时间
2022年12月25日
07：10：53

北京时间
2022年12月25日
12：10：53

答案解析收藏纠错 + 选题
13. (2023七上·婺城期末) 比较大小：52°15′(填“＞”“＜”或“＝”)52.15°．

答案解析收藏纠错 + 选题
14. (2023七上·婺城期末) 若代数式x－2y的值是4，则代数式1－2x＋4y的值为．

答案解析收藏纠错 + 选题
15. (2023七上·婺城期末) 如图，将一副三角尺的顶点重合放置，三角尺AOB绕点O旋转．当∠BOC＝ $\text{[math]}$ ∠COD时，∠AOD＝．

答案解析收藏纠错 + 选题
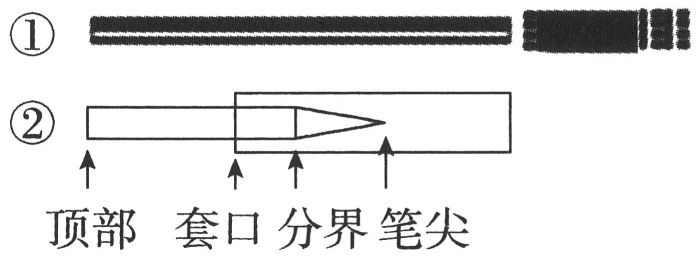
16. (2023七上·婺城期末) 如图①，小盛买了一支铅笔和一个铅笔套．未开始使用时，铅笔的长度是铅笔套长度的3倍多1 cm，且铅笔比铅笔套长12 cm．如图②，削好铅笔时，笔尖与分界处的水平距离为1.5 cm，用铅笔套套住笔尖可以保护铅笔，套口与分界处的距离为1 cm．
1. （1）铅笔套的长度为cm ．
2. （2）铅笔套既能保护铅笔，又能套在铅笔顶部作延长器使用，且用于保护时套口到分界处的距离与用于延长器时套口到顶部的距离相等．正常情况下，1cm的铅笔平均可以写1000字．写完字后，小盛重新削好铅笔，然后套上铅笔套保护铅笔．此时，小盛发现套口刚好在套上铅笔套的整支笔的三等分点，则小盛写了约字．
答案解析收藏纠错 + 选题

三、解答题(本大题有8个小题，第17~19题每小题6分，第20~21题每小题8分，第22~23题每小题10分，第24题12分，共66分)

17. (2023七上·婺城期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024七上·金东期末) 解方程：
1. （1） 2x＋5＝3(x－1)．
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2023七上·婺城期末)
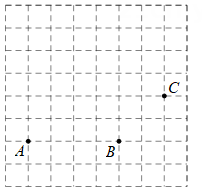
如图，在方格纸中，点A ， B ， C是三个格点(网格线的交点叫做格点)，按要求回答以下问题：
1. （1）画线段BC ．
2. （2）过点C画直线AB的垂线，垂足为D ．
3. （3）线段CD线段CB(填“＞”或“＜”)，理由是．
答案解析收藏纠错 + 选题
20. (2023七上·婺城期末) 已知A＝3x＋xy－2y ，小明在计算2A－B时，误将其按2A＋B计算，结果得到7x＋4xy－y ．
1. （1）求多项式B ．
2. （2）求2A－B的正确结果是多少．
答案解析收藏纠错 + 选题
21. (2023七上·婺城期末)
如图所示为一个长方形游乐场，长是6x(m)，宽为2y(m)，其中半圆形A区为休息区，长方形B区为游泳区，其他地方都是绿地．已知半圆形A区的直径和长方形B区的宽都是y(m)，B区的长是3x(m)．
1. （1）用代数式分别表示该游乐场休息区与游泳区的面积(结果保留π)．
2. （2）当x＝15，y＝20时，若绿化草地每平方米需要费用50元，求这个游乐场绿化草地的费用． (π取3)．
答案解析收藏纠错 + 选题

22. (2023七上·婺城期末) 国庆期间，某超市各个区域都有促销活动，晓琳一家准备去超市购买纸巾，根据以下素材，探索完成任务．

揭秘超市促销：送券和打折哪个更优惠
素材1	纸巾区域推出两种活动： [注：两种活动不能同时参加．] 【活动一】：购物满100元送30元券，满200元送60元券，……，上不封顶，送的券当天有效，需一次性用完．【活动二】：所有商品打八折．
素材2	晓琳家用的两种纸巾的信息(规格与标价)：
		A品牌规格：每袋6包标价：20元/袋	B品牌规格：每箱12包标价：60元/箱
素材3	晓琳家平均三天用1包A品牌纸巾，平均五天用1包B品牌纸巾；晓琳家还剩1袋A品牌纸巾，B品牌纸巾的余量未知．
问题解决
任务1	晓琳家半年(按180天计算)需要消耗A品牌纸巾多少袋？消耗B品牌纸巾多少箱？
任务2	按存半年的用量计算，还需要购买2种纸巾若干，其中B品牌纸巾需购买x箱，若选择活动二，则所需的总费用为元(用含x的代数式表示)．
任务3	晓琳突然想起家中已没有B品牌纸巾，按半年所需的用量来购买，请探索送券和打折哪个更优惠，并写出探索过程．

答案解析收藏纠错 + 选题

23. (2023七上·婺城期末) 已知代数式(a＋4)x³＋6x²－2x＋5是关于x的二次多项式，且二次项系数为b，数轴上A，B两点所对应的数分别是a和b
1. （1） a＝，b＝．
2. （2）有一动点P从点A出发，第一次向左运动1个单位，然后第二次在新的位置向右运动2个单位，再在此位置第三次向左运动3个单位，……，按照这样的规律不断地左右运动，第2023次运动后，点P所对应的数为．
3. （3）若点A以每秒2个单位的速度向左运动，同时，点B以每秒3个单位的速度向右运动．动点D从原点开始以每秒m(m＞0)个单位的速度向左运动，当点D与点A重合时，点D停止运动．在运动过程中，2AD-BD的值始终保持不变，求m的值．
答案解析收藏纠错 + 选题
24. (2023七上·婺城期末) 如图，∠AOB是平角，射线OM从OA开始，先按顺时针方向绕点O向射线OB旋转，到达OB后再绕点O按逆时针方向向射线OA旋转，速度为6°/s ．同时，射线ON从OB开始，以3°/s的速度绕点O按逆时针方向向OA旋转，当ON到达OA时，射线OM与ON都停止运动．设旋转时间为t(s)．
1. （1）当t＝12时，判断射线OM是否是∠AON的平分线，并说明理由．
2. （2）若射线OM与射线ON垂直，求∠BON的度数．
3. （3）在运动过程中，是否存在某一时刻，使得∠BON是∠MON的2倍？若存在，求t的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省金华市婺城区2022-2023学年七年级上学期数学学业...

副标题：

*注意事项：

浙江省金华市婺城区2022-2023学年七年级上学期数学学业...

试题分析

总体分析

题量分析

难度分析

知识点分析