 B .
B .  C .
C .  D .
D . 
下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )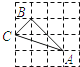
 B .
B . 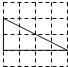 C .
C .  D .
D . 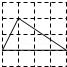
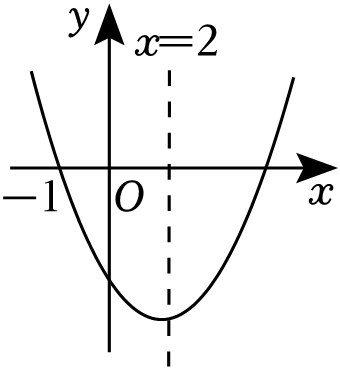
①abc>0;
②a+2c<﹣b;
③c﹣3a=0;
④直线y=m可能与y=|ax2+bx+c|有4个交点;
⑤若点M(x1 , y2),点N(x1 , y2)是抛物线上的两点,若x1<x2 , 则y1<y2 .
其中正确的有( )
①求⊙O的半径长;
②若点G是AF的中点,求DF的长.
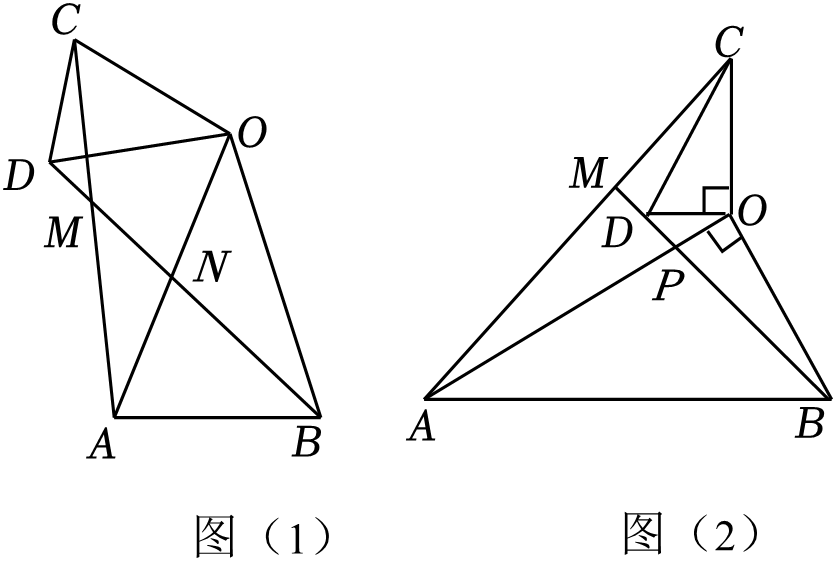
如图(1),在△OAB和△OCD中,OA=OB , OC=OD , ∠AOB=∠COD=40°,连接AC、BD交于点M . 填空:
①的值为 ;②∠AMB的度数为 .
如图(2),在△OAB和△OCD中,∠AOB=∠COD=90°, , 连接AC , 交BD的延长线于点M . 请求出
的值及∠AMB的度数,并说明理由.