
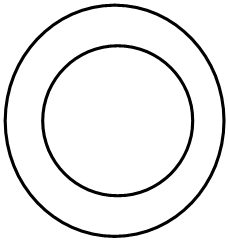
 D .
D . 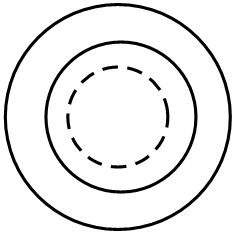
试验总次数 | 100 | 200 | 300 | 500 | 1500 | 2000 | 3000 |
落在“心形线”内部的次数 | 61 | 93 | 165 | 246 | 759 | 996 | 1503 |
落在“心形线”内部的频率 | 0.610 | 0.465 | 0.550 | 0.492 | 0.506 | 0.498 | 0.501 |
根据表中的数据,估计随机投放一点落在“心形线”内部的概率为( )





列表:
x | … | 1 | 2 | 3 | 4 | 6 | … |
y | … | 6 | 3 | m | 1.5 | 1 | … |
上面表格中m的值是 ▲ ;
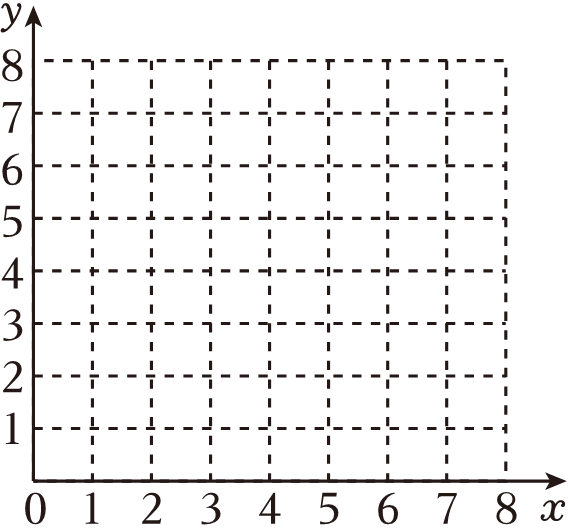
描点:在如图所示的平面直角坐标系中描出相应的点;
连线:用光滑的曲线顺次连接各点,即可得到该函数的图象.
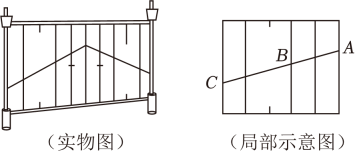
项目主题:守护生命,“数”说安全.
项目背景:随着社会的发展,安全问题变得日益重要.某校为了提高学生的安全意识,开展以“守护生命,'数'说安全”为主题的项目式学习活动.创新小组通过考察测量、模拟探究和成果迁移等环节,开展地下弯道对通行车辆长度的限制研究.
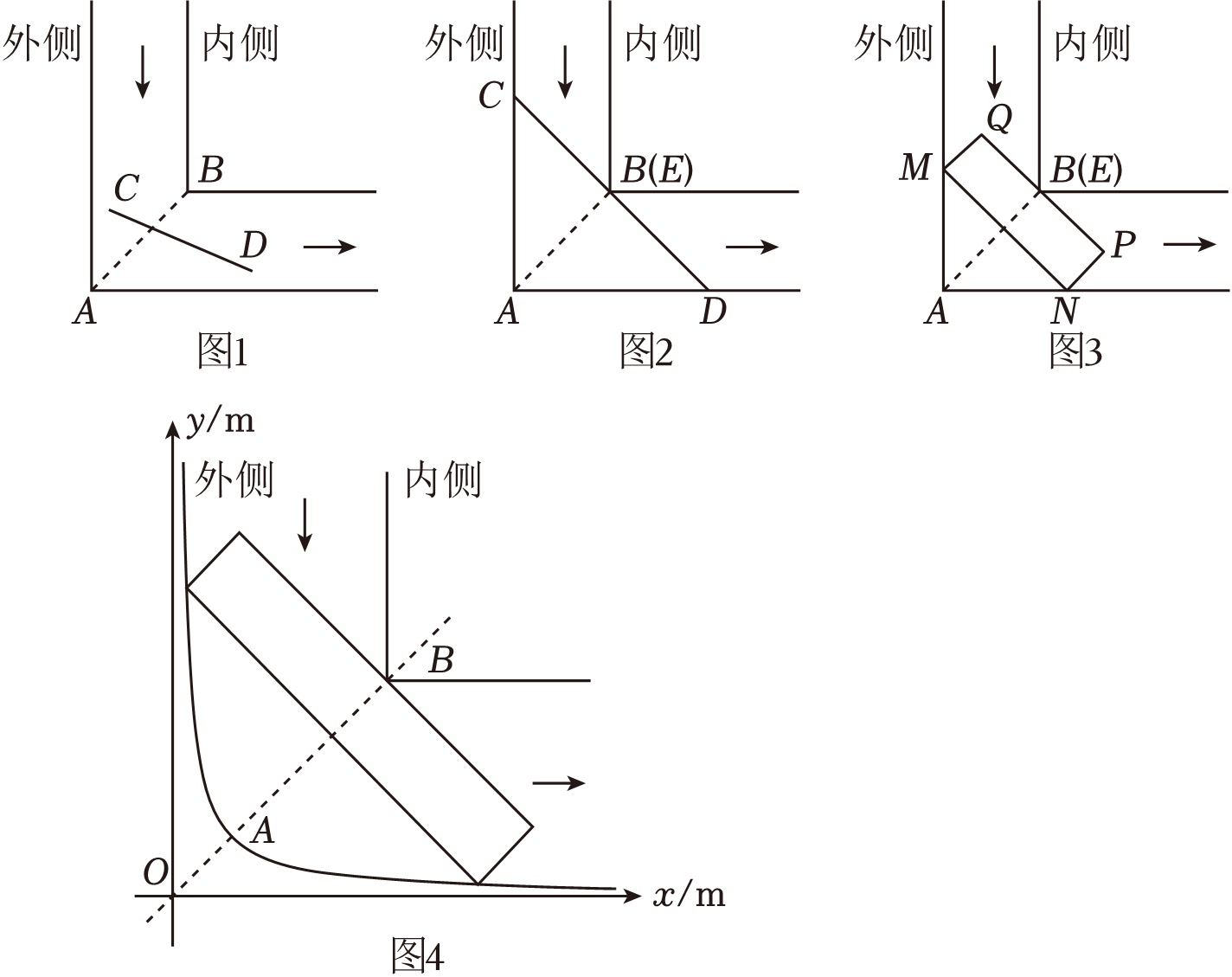
如图1,创新小组所选取弯道的内、外侧均为直角,道路宽均为4m,则AB=m;
如果汽车在行驶中与弯道内、外侧均无接触,则可安全通过.
创新小组用线段模拟汽车通过宽度相同的直角弯道,探究发现:
①当CD<2AB时(如图1),线段CD能通过直角弯道;
②当CD=2AB时,必然存在线段CD的中点E与点B重合的情况,线段CD恰好不能通过直角弯道(如图2).此时,∠ADC的度数是 ;③当CD>2AB时,线段CD不能通过直角弯道.
如图4,某弯道外侧形状可近似看成反比例函数y=(x>0)的图象,其对称轴交图象于点A.弯道内侧的顶点B在射线OA上,两边分别与x轴,y轴平行,OA=2m,AB=4
m.创新小组探究发现通过该弯道的原理与通过直角弯道类似.有一辆长为bm,宽为2m的汽车需要安全通过该弯道,则b的最大整数值为 .(参考数据:
≈1.4,
≈1.7,
≈2.2,
≈2.6)
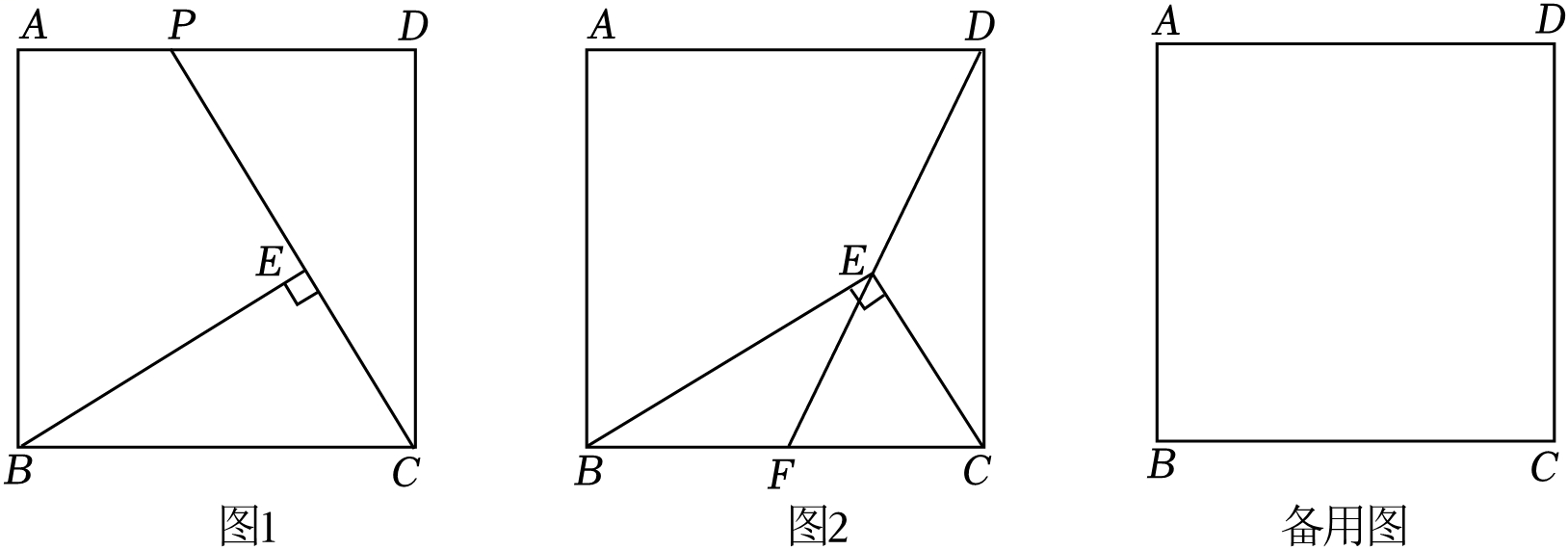
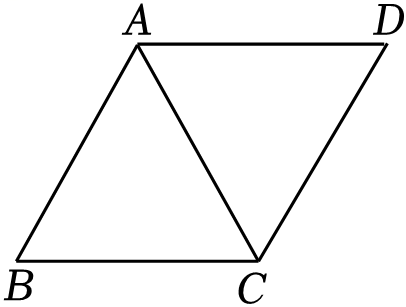
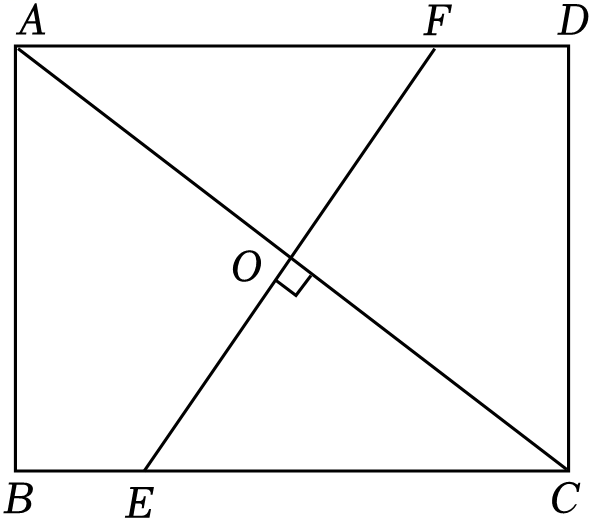
如图1,延长CE交AD于点P.求证:△BEC∽△CDP;
如图2,连接DE并延长交BC于点F,当点F是BC的中点时,求的值;
连接DE并延长交BC于点F,DF把∠BEC分成两个角,当这两个角的度数之比为1:2时,请直接写出的值.