江西省南昌市经济技术开发区2023-2024学年九年级上学期...

更新时间：2024-03-19 浏览次数：9 类型：月考试卷

一、选择题（本大题共6题，每小题3分，共计18分．在每小题列出的四个选项中只有一项是最符合题目要求的）

1. (2023九上·南昌月考) 如图所示图形中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023九上·南昌月考) 若 $\text{[math]}$ 分别是一元二次方程 $\text{[math]}$ 的两个根，则 $\text{[math]}$ 的值是（）．

A . 6 B . $\text{[math]}$ C . 5 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·南昌月考) 把拋物线 $\text{[math]}$ 的图象向上平移2个单位，再向右平移3个单位，所得函数解析式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·南昌月考) 据悉，尽管巴以冲突带来的地缘风险加深了市场对原油供应短缺的担忧，参考原油变化率仍处于负值区间，2023年10月24日，新一轮成品油调价窗口开启，零售限价或遇“二连跌”，若92#汽油连续两次降价 $\text{[math]}$ 后售价由8.1元降低至7.8元，下列所列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·南昌月考) 如图， $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转得到 $\text{[math]}$ ，若 $\text{[math]}$ ，当点 $\text{[math]}$ 怡好在 $\text{[math]}$ 上时，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九上·南昌月考) 如图，在 $\text{[math]}$ 中，动弦 $\text{[math]}$ 与直径 $\text{[math]}$ 相交于点 $\text{[math]}$ 且总有 $\text{[math]}$ ，则 $\text{[math]}$ 的值（）

A . 随着 $\text{[math]}$ 的增大而增大 B . 随着 $\text{[math]}$ 的增大而减小 C . 随着 $\text{[math]}$ 的增大先增大后减小 D . 保持不变

答案解析收藏纠错 + 选题

二、填空题（本大题共6题，每小题3分，共计18分）

7. (2023九上·南昌月考) 已知 $\text{[math]}$ 是方程 $\text{[math]}$ 的解，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
8. (2023九上·南昌月考) 点 $\text{[math]}$ 与点 $\text{[math]}$ 关于原点对称，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
9. (2023九上·南昌月考) 如图1， $\text{[math]}$ 为 $\text{[math]}$ 的直径， $\text{[math]}$ 为 $\text{[math]}$ 的弦， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
10. (2023九上·南昌月考) $\text{[math]}$ 是方程 $\text{[math]}$ 的两根，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
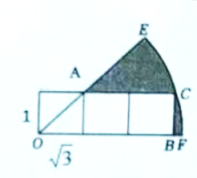
11. (2023九上·南昌月考) 如图2，在扇形 $\text{[math]}$ 中放置有三个全等的矩形方格，点 $\text{[math]}$ 为扇形的圆心，格点 $\text{[math]}$ 分别在扇形的两条半径和弧上，已知每个矩形方格的长和宽分别为 $\text{[math]}$ 和1，则阴影部分的面积为．

答案解析收藏纠错 + 选题
12. (2023九上·南昌月考) 已知等腰 $\text{[math]}$ 接于半径为5的 $\text{[math]}$ ，圆心 $\text{[math]}$ 到 $\text{[math]}$ 的距离为3，则这个等腰 $\text{[math]}$ 中底边上的高可能是．

答案解析收藏纠错 + 选题

三、解答题（本大题共5题，每小题6分，共计30分）

13. (2023九上·南昌月考) 解方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
14. (2023九上·南昌月考) 通过配方，确定抛物线 $\text{[math]}$ 的顶点坐标，并直接写出当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围．

答案解析收藏纠错 + 选题
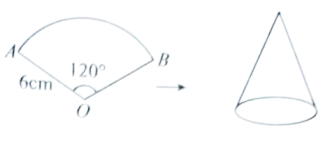
15. (2023九上·南昌月考) 如图所示，已知扇形 $\text{[math]}$ 的半径为 $\text{[math]}$ ，圆心角的度数为 $\text{[math]}$ ，若将此扇形围成一个圆锥侧面，求围成的圆锥的高以及圆锥的全面积．

答案解析收藏纠错 + 选题
16. (2023九上·南昌月考) 如图，已知 $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ ，请仅用无刻度的直尺，按下列要求画图（保留画图痕迹）．
1. （1）在图1的 $\text{[math]}$ 上作点D，使 $\text{[math]}$ 为等腰直角三角形；
2. （2）在图2的 $\text{[math]}$ 上作点M，N，使四边形 $\text{[math]}$ 为正方形．
答案解析收藏纠错 + 选题
17. (2023九上·南昌月考) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的弦， $\text{[math]}$ ，垂足分别为 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1） $\text{[math]}$ 与 $\text{[math]}$ 相等吗？为什么？
2. （2）判断 $\text{[math]}$ 与 $\text{[math]}$ 是否相等，并说明理由．
答案解析收藏纠错 + 选题

四、解答题（本大题共3题，每小题8分，共计24分）

18. (2023九上·南昌月考) 定义：若一元二次方程 $\text{[math]}$ 满足 $\text{[math]}$ ．则称此方程为“蚊龙”方程．
1. （1）当 $\text{[math]}$ 时，判断此时“蛟龙”方程 $\text{[math]}$ 解的情况，并说明理由．
2. （2）若“蛟龙”方程 $\text{[math]}$ 有两个相等的实数根，请解出此方程，
答案解析收藏纠错 + 选题
19. (2023九上·南昌月考) 如图，点 $\text{[math]}$ 是正方形 $\text{[math]}$ 内的一点，连接 $\text{[math]}$ ．将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 到 $\text{[math]}$ 的位置．
1. （1）设 $\text{[math]}$ 的长为 $\text{[math]}$ 的长为 $\text{[math]}$ ，求 $\text{[math]}$ 旋转到 $\text{[math]}$ 的过程中边 $\text{[math]}$ 所扫过区域（图中阴影部分）的面积．
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
20. (2023九上·南昌月考) 商场将进货价为40元每件的某商品以50元售出，平均每月能售出700件，调查表明：售价在50元至100元范围内，这种商品的售价每上涨1元，其销售量就将减少10件，设商场决定每件商品的售价为 $\text{[math]}$ 元．
1. （1）该商场平均每月可售出件商品（用含 $\text{[math]}$ 的代数式表示）；
2. （2）商品售价定为多少元时，每月销售利润最大？
3. （3）该商场决定每销售一件商品就捐赠 $\text{[math]}$ 元利润 $\text{[math]}$ 给希望工程，通过销售记录发现，每件商品销售价格大于85元时，扣除捐款后每天的利润随 $\text{[math]}$ 增大而减小，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题

五、解答题（本大题共2题，每小题9分，共计18分）

21. (2023九上·南昌月考) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，点 $\text{[math]}$ 是劣弧 $\text{[math]}$ 中点， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ．连接 $\text{[math]}$ $\text{[math]}$ 与 $\text{[math]}$ 的延长线相交于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）求证： $\text{[math]}$ ；
3. （3）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
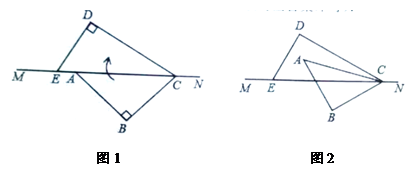
22. (2023九上·南昌月考) 将一副直角三角板如图1，摆放在直线 $\text{[math]}$ 上（直角三角板 $\text{[math]}$ 和直角三角板 $\text{[math]}$ ， $\text{[math]}$ ），保持三角板 $\text{[math]}$ 不动，将三角板 $\text{[math]}$ 绕点 $\text{[math]}$ 以每秒 $\text{[math]}$ 的速度顺时针旋转，旋转时间为秒，当 $\text{[math]}$ 与射线 $\text{[math]}$ 重合时停止旋转．
1. （1）如图2，当 $\text{[math]}$ 为 $\text{[math]}$ 的角平分线时，求此时的值；
2. （2）当 $\text{[math]}$ 旋转至 $\text{[math]}$ 的内部时，求 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系；
3. （3）在旋转过程中，当三角板 $\text{[math]}$ 的其中一边平行于三角板 $\text{[math]}$ 的某一边时，求此时t等于（直接写出答案即可）．
答案解析收藏纠错 + 选题

六、解答题（本大题共1题，每小题12分，共计12分）

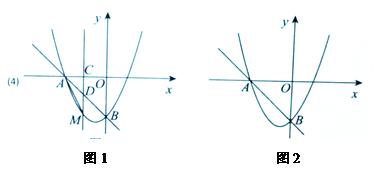
23. (2023九上·南昌月考) 如图，在平面直角坐标系中，一次函数 $\text{[math]}$ 的图像与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，二次函数的图象 $\text{[math]}$ 经过点A、B ．
1. （1） $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）若点 $\text{[math]}$ 是第三象限内抛物线上的一动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 垂直于 $\text{[math]}$ 轴，垂足为点 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，当 $\text{[math]}$ 时：
  ①求点 $\text{[math]}$ 的坐标；
  ②直线 $\text{[math]}$ 上是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ 为直角三角形？若存在，直接写出符合条件的所有点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
3. （3）抛物线上是否存在点 $\text{[math]}$ （不与点 $\text{[math]}$ 重合），使得 $\text{[math]}$ 四点共圆，如果存在求出点 $\text{[math]}$ 的坐标，如果不存在，请说明理由．
答案解析收藏纠错 + 选题