湖南省邵阳市新宁县思源中学2023-2024学年七年级上学期...

更新时间：2024-03-19 浏览次数：12 类型：月考试卷

一、选择题（本大题共10个小题，每小题3分，共30分）

1. (2023七上·新宁月考) $\text{[math]}$ 的绝对值是（）

A . 2023 B . $\text{[math]}$ C . 0 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023七上·公安期中) 下列各代数式中是五次单项式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·长沙模拟) 第24届冬季奥林匹克运动会已经画上圆满句号，北京成为历史上首座“双奥之城”，再一次见证了竞技体育的荣耀与梦想，凝聚了人类社会的团结与友谊，2022年2月4日的北京冬奥会开幕式在全国44个上星频道播出，收看电视直播观众规模约为 $\text{[math]}$ 人，将 $\text{[math]}$ 用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023七上·新宁月考) 某冷冻厂的一个冷库，现在的室温是 $\text{[math]}$ ，现有一批食品，需在 $\text{[math]}$ 下冷成．如果每小时能降温 $\text{[math]}$ ，要降到所需温度需（）小时

A . 6 B . $\text{[math]}$ C . 7 D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023七上·新宁月考) 下列变形中，正确的是（）

A . 若 $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ，则 $\text{[math]}$ D . 若 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023七上·新宁月考) 下图立体图形中是圆锥的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2023七上·新宁月考) 在等式 $\text{[math]}$ 中，“□”内填上一个数字，可使等式成立．则“□”内数字应为（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
8. (2023七上·新宁月考) 已知方程 $\text{[math]}$ 的解是5，则a的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 13 D . 17

答案解析收藏纠错 + 选题
9. (2023七上·新宁月考) 按如图所示的运算程序，若输入 $\text{[math]}$ 的值是 $\text{[math]}$ ，则输出的结果是（）

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . 7

答案解析收藏纠错 + 选题
10. (2023七上·新宁月考) a是不为2的有理数，我们把 $\text{[math]}$ 称为a的“伴随数”，如3的“伴随数”是 $\text{[math]}$ ， $\text{[math]}$ 的“伴随数”是 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的“伴随数”， $\text{[math]}$ 是 $\text{[math]}$ 的“伴随数”， $\text{[math]}$ 是 $\text{[math]}$ 的“伴随数”，…，依此类推，则 $\text{[math]}$ 等于（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题

二、填空题（本大题共6个小题，每小题3分，共18分）

11. (2023七上·新宁月考) 比较大小： $\text{[math]}$ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2023七上·新宁月考) 若 $\text{[math]}$ 与 $\text{[math]}$ 的和仍然是一个单项式，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2023七上·新宁月考) 已知方程 $\text{[math]}$ 是关于 $\text{[math]}$ 的一元一次方程，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
14. (2024七下·丰城开学考) 华为mate60pro手机一经问世，由于其性能遥遥领先于其它品牌手机，市场出现供不应求，导致消费者需加价才能买到手机，若该手机加价 $\text{[math]}$ 以后，每台售价为7920元，则该品牌手机每台原价为元．

答案解析收藏纠错 + 选题
15. (2023七上·新宁月考) 如果 $\text{[math]}$ 与 $\text{[math]}$ 互为相反数，那么 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
16. (2023七上·新宁月考) 七年级一位同学用围棋棋子摆出“湖南师大附中教育集团”中的“大”字，如图①，图②，图③，…，按照某种规律摆成的一行“大”字，按照这种规律，第 $\text{[math]}$ 个“大”字中的棋子个数是．

答案解析收藏纠错 + 选题

三、解答题（共9小题，17，18，19每小题6分，20，21每小题8分，22，23每小题9分，24，25每小题10分，共72分）

17. (2023七上·新宁月考) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2023七上·新宁月考) 解方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2024七下·路南开学考) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2023七上·新宁月考) 世界杯比赛中，根据场上攻守形势，守门员会在门前来回跑动，如果以球门线为基准，向前跑记作正数，返回则记作负数，一段时间内，某守门员的跑动情况记录如下（单位：m）： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．（假定开始计时时，守门员正好在球门线上）
1. （1）守门员最后是否回到球门线上？
2. （2）守门员离开球门线的最远距离达多少米？
3. （3）如果守门员离开球门线的距离超过10米（不包括10米），则对方球员挑射极可能造成破门．请问在这一时间段内，对方球员有几次挑射破门的机会？
答案解析收藏纠错 + 选题
21. (2023七上·新宁月考) 小明房间的窗户如图所示，是长为b米，宽为a米的长方形．其中上方的装饰物由两个四分之一圆和一个半圆组成（它们的半径相同）．
1. （1）用代数式表示窗户中能射进阳光的部分的面积是多少？（窗框面积忽略不计，保留π）
2. （2）若 $\text{[math]}$ 米， $\text{[math]}$ 米时，求窗户中能射进阳光的部分的面积是多少？（保留π）
答案解析收藏纠错 + 选题
22. (2023七上·新宁月考) 阅读材料：我们知道， $\text{[math]}$ ，类似地，我们把 $\text{[math]}$ 看成一个整体，则 $\text{[math]}$ ． “整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．
1. （1）把 $\text{[math]}$ 看成一个整体，求合并 $\text{[math]}$ 的结果；
2. （2）已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
23. (2023七上·新宁月考) 在“清洁乡村”活动中，村里需购买一些垃圾桶，商家给出了两种购买垃圾桶方案：
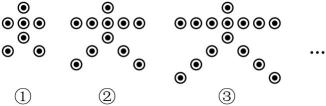
方案一：买分类垃圾桶，需要费用4000元，以后每月的垃圾处理费用300元；
方案二：买不分类垃圾桶，需要费用1000元，以后每月的垃圾处理费用600元．
设交费时间为 $\text{[math]}$ 个月，方案一的购买费和垃圾处理费共为 $\text{[math]}$ 元，方案二的购买费和垃圾处理费共为 $\text{[math]}$ 元．
1. （1）分别用 $\text{[math]}$ 表示 $\text{[math]}$ ；
2. （2）若交费时间为1年，哪种方案更省钱？并说明理由；
3. （3）交费时间多长时，两种方案费用相等？
答案解析收藏纠错 + 选题
24. (2023七上·新宁月考) 有这样一道题：关于 $\text{[math]}$ 的多项式 $\text{[math]}$ 与 $\text{[math]}$ 的和的值与字母 $\text{[math]}$ 的取值无关，求 $\text{[math]}$ 的值．通常的解题方法是：两式相加后，把 $\text{[math]}$ 看作字母， $\text{[math]}$ 看作系数合并同类项，因为代数式的值与 $\text{[math]}$ 的取值无关，所以含 $\text{[math]}$ 项的系数为0，即 $\text{[math]}$ ，所以 $\text{[math]}$ ，则 $\text{[math]}$ ．
1. （1）【初步尝试】
  若关于 $\text{[math]}$ 的多项式 $\text{[math]}$ 的值与 $\text{[math]}$ 无关，求 $\text{[math]}$ 的值．
2. （2）【深入探究】
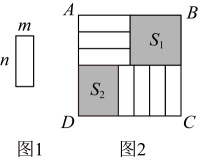
  7张如图1的小长方形，长为 $\text{[math]}$ ，宽为 $\text{[math]}$ ，按照图2方式不重叠地放在大长方形 $\text{[math]}$ 内，大长方形中未被覆盖的两个部分（图中阴影部分），设右上角的面积为 $\text{[math]}$ ，左下角的面积为 $\text{[math]}$ ．
  ①若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
  ②当 $\text{[math]}$ 的长变化时， $\text{[math]}$ 的值始终保持不变，求 $\text{[math]}$ 与 $\text{[math]}$ 的等量关系．
答案解析收藏纠错 + 选题
25. (2023七上·新宁月考) 我们知道 $\text{[math]}$ ，它的几何意义是数轴上表示4的点与原点（即表示0的点）之间的距离，又如式子 $\text{[math]}$ ，它的几何意义是数轴上表示7的点与表示3的点之间的距离．也就是说，在数轴上，如果点 $\text{[math]}$ 表示的数记为 $\text{[math]}$ ，点 $\text{[math]}$ 表示的数记为 $\text{[math]}$ 则 $\text{[math]}$ 两点间的距离就可记作 $\text{[math]}$ ．
回答下列问题：
1. （1）数轴上表示 $\text{[math]}$ 和2的两点之间的距离是；
2. （2）小明在草稿纸上画了一条数轴，并折叠数轴，表示2的点与表示 $\text{[math]}$ 的点重合．如果 $\text{[math]}$ （ $\text{[math]}$ 在 $\text{[math]}$ 的左侧）两点之间的距离为2024，且 $\text{[math]}$ 两点经过上述折叠后重合，则 $\text{[math]}$ 表示的数分别是多少？
3. （3）如图，在数轴上剪下6个单位长度（从 $\text{[math]}$ 至5）的一条线段，并把这条线段沿某点向左折叠，然后在重叠部分的某处剪一刀得到三条线段，发现这三条线段的长度之比为 $\text{[math]}$ ，则折痕处对应的点表示的数可能是多少？
答案解析收藏纠错 + 选题