一、单选题:(本大题共8小题,每小题5分,共40 分.在每小题四个选项中 ,只有一项是符合题目要求的)
-
-
-
-
4.
(2023高三上·闽清月考)
2021年某省高考体育百米测试中,成绩全部介于12秒与18秒之间,抽取其中100个样本,将测试结果按如下方式分成六组:第一组

, 第二组

, …,第六组

, 得到如下频率分布直方图,则该100名考生的成绩的平均数和中位数(保留一位小数)分别是( )

A . 15.2 15.4
B . 15.1 15.4
C . 15.1 15.3
D . 15.2 15.3
-
-
-
-
8.
(2023高三上·闽清月考)
2023年夏天贵州榕江的村超联赛火爆全国,吸引了国内众多业余球队参赛.现有六个参赛队伍代表站成一排照相,如果贵阳折耳根队与柳州螺蛳粉队必须相邻,同时南昌拌粉队与温江烤肉队不能相邻,那么不同的站法共有( )种.
A . 144
B . 72
C . 36
D . 24
二、多选题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中 ,有多项是符合题目要求的。正确选项全对得5分,正确选项不全得2分,有错误选项得0分)
-
A . 若 是第一象限角,则
是第一象限角,则 B . 终边经过点
B . 终边经过点 的角的集合是
的角的集合是 C . 对
C . 对 ,
,  恒成立
D . 若
恒成立
D . 若 , 且
, 且 , 则
, 则
-
A .  B .
B .  平面ABCD
C . 三棱锥
平面ABCD
C . 三棱锥 的体积为定值
D .
的体积为定值
D .  的面积与
的面积与 的面积相等
的面积相等
-
-
A . 若 服从正态分布
服从正态分布 , 则
, 则 B . 已知随机变量
B . 已知随机变量 服从二项分布
服从二项分布 , 且
, 且 , 随机变量
, 随机变量 服从正态分布
服从正态分布 , 若
, 若 , 则
, 则 C . 若
C . 若 服从超几何分布
服从超几何分布 , 则期望
, 则期望 D . 若
D . 若 服从二项分布
服从二项分布 , 则方差
, 则方差
三、填空题:本大题共4小题,每小题5分,共20分。
-
-
14.
(2023高三上·闽清月考)
已知圆锥的顶点为

, 母线

所成角的余弦值为

,

与圆锥底面所成角为

, 若

的面积为

, 则该圆锥的侧面积为
.
-
15.
(2023高三上·闽清月考)
已知椭圆

与双曲线

(

,

)具有相同的左、右焦点

、

, 点

为它们在第一象限的交点,动点

在曲线

上,若记曲线

,

的离心率分别为

,

, 满足

, 且直线

与

轴的交点的坐标为

, 则

的最大值为
.
-
四、解答题:本大题共6小题,共70 分.解答应写出文字说明,证明过程或演算步骤。
-
-
(1)
判断

的单调性,并证明;
-
(2)
解关于

的不等式

.
-
-
(1)
求证:

平面

;
-
(2)
设正方体的棱长为1,求三棱锥

的体积.
-
-
(1)
求

的模;
-
(2)
若

与

互相垂直,求
λ的值.
-
20.
(2023高三上·闽清月考)
在

中,角

,

,

的对边分别为

,

,

, 面积为

, 在下列三个条件中任选一个,解答下面的问题.①

, ②

, ③

.
-
(1)
求角

的大小;
-
-
-
(1)
求

与

通项公式;
-
-
22.
(2024高三上·南宁月考)
某工厂注重生产工艺创新,设计并试运行了甲、乙两条生产线.现对这两条生产线生产的产品进行评估,在这两条生产线所生产的产品中,随机抽取了300件进行测评,并将测评结果(“优”或“良”)制成如下所示列联表:
| 良 | 优 | 合计 |
甲生产线 | 40 | 80 | 120 |
乙生产线 | 80 | 100 | 180 |
合计 | 120 | 180 | 300 |
-
(1)
通过计算判断,是否有

的把握认为产品质量与生产线有关系?
-
(2)
现对产品进行进一步分析,在测评结果为“良”的产品中按生产线用分层抽样的方法抽取了6件产品.若在这6件产品中随机抽取3件,求这3件产品中产自于甲生产线的件数

的分布列和数学期望.
附表及公式:

| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |

| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
其中 .
.
-
-
(1)
求双曲线

的方程;
-
(2)
记

为坐标原点,过点

且斜率为

的直线

与双曲线

相交于不同的两点

, 求

的面积.

 B .
B . 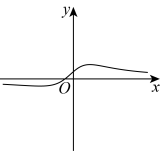 C .
C .  D .
D . 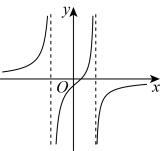
.