一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
A . 2014
B . 2015
C . 2023
D . 2024
-
-
3.
(2024·扬州模拟)
在

中,角

,

,

所对的边分别为

,

,

, 若

, 且

的外接圆的半径为

, 则

面积的最大值为( )
-
-
A . 0
B . 0或1
C . 2
D . 0或1或2
-
-
7.
(2024·扬州模拟)
对于一个给定的数列

, 令

, 则数列

称为数列

的一阶商数列,再令

, 则数列

是数列

的二阶商数列.已知数列

为

,

,

,

,

, ...,且它的二阶商数列是常数列,则

( )
-
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
-
A .  B .
B .  的前
的前 项和中
项和中 最小
C .
最小
C .  的最小值为
的最小值为 D .
D .  的最大值为0
的最大值为0
-
A .  为偶函数
B .
为偶函数
B .  是
是 的一个单调递增区间
C .
的一个单调递增区间
C .  D . 当
D . 当 时,
时,
-
三、填空题:本题共4小题,每小题5分,共20分.
-
-
-
15.
(2024·扬州模拟)
已知点
P是直线

:

和

:

(
m ,

,

)的交点,点
Q是圆
C:

上的动点,则

的最大值是
.
-
16.
(2024·扬州模拟)
已知直线

与双曲线

:


的两条渐近线分别交于点

,

(不重合)线段

的垂直平分线过点

, 则双曲线

的离心率为
.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
-
-
(2)
化简求值:

-
18.
(2024·扬州模拟)
在

中,已知角
A ,
B ,
C的对边分别为
a ,
b ,
c , 且
a ,
b ,
c是公差为1的等差数列.
-
(1)
若

, 求

的面积;
-
(2)
是否存在正整数
a , 使

为钝角三角形?若存在,求
a的值;若不存在,说明理由.
-
-
-
(2)
若函数

有两个零点,求实数

的取值范围.
-
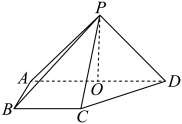
20.
(2024·扬州模拟)
如图,在四棱锥

中,则面

底面

, 侧棱

, 底面

为直角梯形,其中

,

,

,

为

中点.
-
(1)
求证:

平面

;
-
(2)
求异面直线

与

所成角的大小.
-
-
(1)
求

的方程;
-
(2)
①若

, 求

的面积;
②证明:当 面积最大时,
面积最大时, 必定经过
必定经过 的某个顶点.
的某个顶点.
-
22.
(2024·扬州模拟)
在三维空间中,立方体的坐标可用三维坐标

表示,其中

. 而在
n维空间中

, 以单位长度为边长的“立方体”的顶点坐标可表示为
n维坐标

, 其中

. 现有如下定义:在
n维空间中两点间的曼哈顿距离为两点

与

坐标差的绝对值之和,即为

. 回答下列问题:
-
-
(2)
在
n维“立方体”中任取两个不同顶点,记随机变量
X为所取两点间的曼哈顿距离
①求出X的分布列与期望;
②证明:在n足够大时,随机变量X的方差小于 .
.
(已知对于正态分布 , P随X变化关系可表示为
, P随X变化关系可表示为 )
)
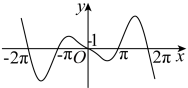 B .
B .  C .
C . 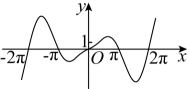 D .
D . 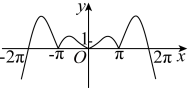
面积最大时,
必定经过
的某个顶点.
.
, P随X变化关系可表示为
)