题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

广西壮族自治区防城港市防城区2023-2024学年九年级上...

更新时间：2024-02-28 浏览次数：32 类型：期末考试

一、选择题（共12小题，每小题3分，共36分.在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑）

1. (2024九上·防城期末) 下列标志中，既是轴对称图形又是中心对称图形的为（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九上·防城期末) 下列事件中，属于必然事件的是（）

A . 明天会下雨 B . 抛一枚硬币，正面朝上 C . 地球每天都在自转 D . 打开电视机，正在播放广告

答案解析收藏纠错 + 选题
3. (2024九上·防城期末) 平面直角坐标系内，点 $\text{[math]}$ 关于原点对称点的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九上·防城期末) 抛物线 $\text{[math]}$ 的顶点坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九上·防城期末) 关于x的一元二次方程 $\text{[math]}$ 有实数根，则m的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九上·防城期末) 用配方法解方程 $\text{[math]}$ ，变形后的结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九上·防城期末) 在 $\text{[math]}$ 中，P是弦 $\text{[math]}$ 的中点， $\text{[math]}$ 是过点P的直径，则下列结论中不正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九下·凉州模拟) 抛物线 $\text{[math]}$ 向右平移2个单位，再向下平移3个单位，得到新的抛物线解析式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九上·防城期末) 下列说法正确的是（）

A . 抛一枚质地均匀的硬币8次，其中正面朝上的有5次，所以正面朝上的概率为 $\text{[math]}$ B . 某种彩票中奖的概率是1%，因此买100张该种彩票一定会中奖 C . 天气预报说明天下雨的概率是50%，所以明天将有一半时间在下雨 D . 抛掷一枚图钉，钉尖触地和钉尖朝上的概率不相等

答案解析收藏纠错 + 选题
10. (2024九上·防城期末) 如图，Rt△ABC中，∠ACB＝90°，BC＝4，AC＝3，将△ABC绕点B逆时针旋转得 $\text{[math]}$ ，若点 $\text{[math]}$ 在AB上，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . 4 C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
11. (2024九上·防城期末) 有一人患了流感，经过两轮传染后共有121人患了流感，每轮传染中平均一个人传染了几个人？设每轮传染中平均一个人传染了x个人，下列所列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024九上·防城期末) 已知如图，在正方形 $\text{[math]}$ 中，点A、C的坐标分别是 $\text{[math]}$ 和 $\text{[math]}$ ，点D在 $\text{[math]}$ 的图象上，则k的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题2分，共12分.）

13. (2024九上·防城期末) “明天太阳从西边升起”是事件.

答案解析收藏纠错 + 选题
14. (2024九上·防城期末) 抛物线 $\text{[math]}$ 的顶点坐标是.

答案解析收藏纠错 + 选题
15. (2024九上·防城期末) 关于x的方程 $\text{[math]}$ 的一个根是1，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2024九上·防城期末) 圆锥的底面半径为2，母线长为3，它的侧面积为.

答案解析收藏纠错 + 选题
17. (2024九上·防城期末) 如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠D＝110°，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题
18. (2024九上·防城期末) 四边形 $\text{[math]}$ 是正方形，E ， F分别是 $\text{[math]}$ 和 $\text{[math]}$ 的延长线上的点，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积为.

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，共72分.解答应写出文字说明，证明过程或演算步骤）

19. (2024九上·防城期末)
1. （1）计算： $\text{[math]}$
2. （2）解方程： $\text{[math]}$ .
答案解析收藏纠错 + 选题
20. (2024九上·防城期末) 如图，已知二次函数 $\text{[math]}$ 的图象与x轴交于点 $\text{[math]}$ ， $\text{[math]}$ ，与y轴分别交于C.
1. （1）求点C的坐标；
2. （2）求函数图象的对称轴；
答案解析收藏纠错 + 选题
21. (2024九上·防城期末) 如图， $\text{[math]}$ 三个顶点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）请画出 $\text{[math]}$ 关于原点中心对称的 $\text{[math]}$ ；并写出点 $\text{[math]}$ 的坐标；
2. （2）在（1）的条件下，求扇形 $\text{[math]}$ 的面积（结果保留π）.
答案解析收藏纠错 + 选题
22. (2024九上·防城期末) 一个不透明的布袋里装有3个白球，1个黑球和若干个红球，它们除颜色外其余都相同，从中任意摸出1个球，是白球的概率 $\text{[math]}$ .
1. （1）布袋里红球有多少个?
2. （2）先从布袋中摸出1个球后不放回，再摸出1个球，请用列表或画树状图等方法求出两次摸到的球都是白球的概率.
答案解析收藏纠错 + 选题
23. (2024九上·防城期末) 已知P是 $\text{[math]}$ 外一点， $\text{[math]}$ 交 $\text{[math]}$ 于点C ， $\text{[math]}$ ，弦 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的长；
2. （2）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线.
答案解析收藏纠错 + 选题
24. (2024九上·防城期末) 已知抛物线 $\text{[math]}$ 的图象与x轴交于点 $\text{[math]}$ 和点C ，与y轴交于点 $\text{[math]}$ .
1. （1）求抛物线的解析式；
2. （2）设点P为抛物线的对称轴上一动点，当 $\text{[math]}$ 的周长最小时，求点P的坐标；
答案解析收藏纠错 + 选题
25. (2024九上·防城期末) 【综合与实践】数学来源于生活，同时数学也可以服务于生活.
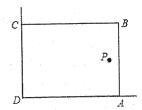
【知识背景】如图，校园中有两面直角围墙，墙角内的P处有一古棵树与墙 $\text{[math]}$ ， $\text{[math]}$ 的距离分别是 $\text{[math]}$ 和 $\text{[math]}$ ，在美化校园的活动中，某数学兴趣小组想借助围墙（两边足够长），用 $\text{[math]}$ 长的篱笆围成一个矩形花园 $\text{[math]}$ （篱笆只围 $\text{[math]}$ ， $\text{[math]}$ 两边），设 $\text{[math]}$ .
【方案设计】设计一个矩形花园，使之面积最大，且要将古棵树P围在花园内（含边界，不考虑树的粗细）.
【解决问题】思路：把矩形 $\text{[math]}$ 的面积S与边长x（即 $\text{[math]}$ 的长）的函数解析式求出，并利用函数的性质来求面积的最大值即可.
1. （1）请用含有x的代数式表示 $\text{[math]}$ 的长；
2. （2）花园的面积能否为 $\text{[math]}$ ?若能，求出x的值，若不能，请说明理由；
3. （3）求面积S与x的函数解析式，写出x的取值范围；并求当x为何值时，花园面积S最大?
答案解析收藏纠错 + 选题
26. (2024九上·防城期末) 【探究与证明】成语“以不变应万变”中蕴含着某种数学原理.
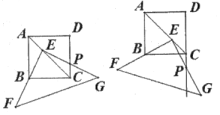
图1 图2
【动手操作】如图1， $\text{[math]}$ 是正方形 $\text{[math]}$ 的对角线，点E是 $\text{[math]}$ 上的一个动点，过点E和B作等腰直角 $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与射线 $\text{[math]}$ 交于点P.
请完成：
1. （1）试判断图1中的 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系；
2. （2）当点P在线段 $\text{[math]}$ 上时，求证： $\text{[math]}$ .
3. （3）【类比操作】如图2，当点P在线段 $\text{[math]}$ 的延长线上时. $\text{[math]}$ 是否还成立?请判断并证明你的结论.
答案解析收藏纠错 + 选题

试卷信息