
 B .
B .  C .
C .  D .
D . 
![]()
 B .
B . 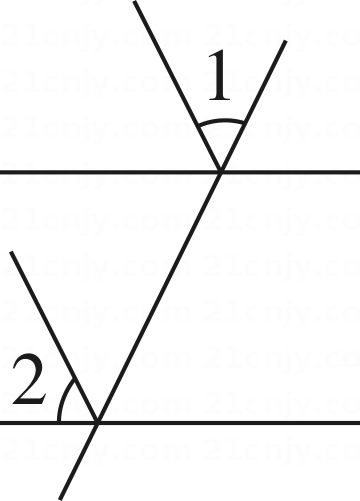 C .
C .  D .
D . 





+15、﹣2、+5、﹣1、﹣3、﹣2.+12、+4、﹣5、+6.

解:∵AB∥CD(已知),
∴∠B= ▲ ( )
∵∠B=∠D=37°(已知)
∴ ▲ =∠D(等量代换)
∴BC∥DE ( ).

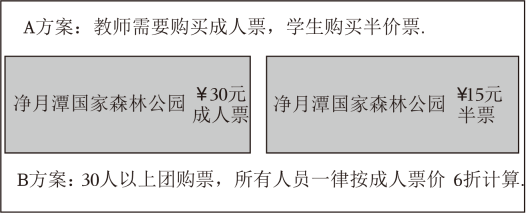
A:元;
B:元.
![]()

【阅读理解】
小明通过观察发现:
x2+x+3→2x2+2x﹣3
前后两个多项式中,含x次数相同项的系数存在相同的倍数关系.
思考:只需求得x2+x的值即可求得2x2+2x的值,进而解决问题.
于是他在做作业时采用了如下方法:
由题意,得x2+x+3=7,则有x2+x=4.
2x2+2x﹣3=2(x2+x)﹣3=2×4﹣3=5.
所以代数式2x2+2x﹣3的值为5.
【方法学习】
这种方法叫整体代入法,是我们在整式求值时常用到的一种方法,即题目已知条件告诉我们的不是单个未知数的值,而是一个或者几个式子的值,让我们根据条件去求其它代数式的值.这个时候,我们要将问题中的式子转化成含有已知式子的形式,然后整体将已知条件代入求值.

【提出问题】小明提出:∠BPD、∠ABP和∠CDP三个角之间存在着什么样的数量关系?
【分析问题】我们学习过平行线的性质,利用平行线的性质可以把∠BPD分成两部分进行研究.
②如图②,已知AB∥CD,点E、F分别是AB、CD上的点,点P位于AB上方,∠PEB=α,∠PFD=β.用含α和β的代数式表示下列各角.
∠P的大小为.如图③,在图②的基础上,若EQ和FQ分别平分∠PEB和∠PFD,则∠Q的大小为.