
a.每天在校体育锻炼时间分布情况:
每天在校体育锻炼时间x | 频数 | 百分比 |
14 | 14% | |
40 | m | |
35 | 35% | |
n | 11% |
b.每天在校体育锻炼时间在这一组的是:
80 81 81 81 82 82 83 83 84 84 84 84 84 85 85 85 85 85
85 85 85 86 87 87 87 87 87 88 88 88 89 89 89 89 89
根据以上信息.回答下列问题:
【参考数据: ,
,
】
与
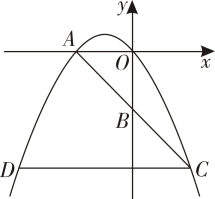
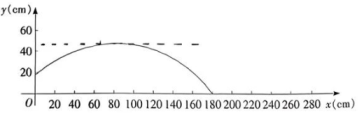
的几组数据如下表所示:
水平距离x(cm) | 0 | 40 | 80 | 120 | 160 | 180 |
竖直高度y(cm) | 18 | 42 | 50 | 42 | 18 | 0 |
根据表中数据,直接写出乒乓球离桌面竖直高度的最大值,并求出满足的函数关系式.
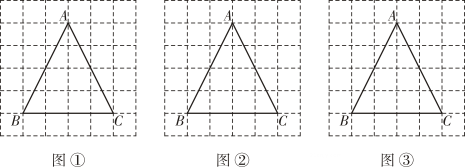
图①  图②
图②  图③
图③