成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数 | 2 | 8 | 17 | 10 | 3 |

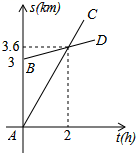
①{-0.4}=-0.4;
②若x+y=n是整数,则[x]+[y]=n或n-1;
③若[x]=1,[y]=2,[z]=3,则[x+y+z]所有可能的值为6,7,8;
④方程3x-{x}=2[x]+3的解为x=3;
⑤[x]+[x+0.5]=[2x]对一切实数x均成立.
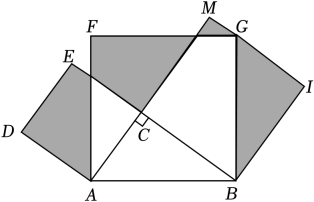
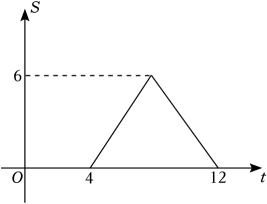

九年级(1)班10名学生的成绩是:96,80,96,86,99,98,92,100,89,82.
九年级(2)班10名学生的成绩在C组中的数据是:94,90,92.
通过数据分析,列表如下:
年级 | 平均数 | 中位数 | 众数 | 方差 |
九年级(1)班 | 91.8 | b | c | 52 |
九年级(2)班 | 92 | 93 | 100 | 50.4 |
九年级(1)班、(2)班抽取的学生竞赛成绩统计表
根据以上信息,解答下列问题:
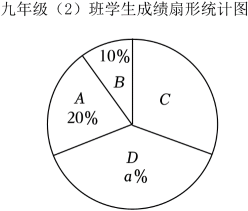
价格类别 | A款玩偶 | B款玩偶 |
进货价(元/个) | 20 | 15 |
销售价(元/个) | 28 | 20 |
设A款玩偶购进x个,获利y元.
例如693,∵3+6=9,∴693是“平衡数”.F(693)=6×3=18.
规定:G(m,n)=sF(m)+tF(n)(s,t均为非零实数,m,n均为平衡数).
已知:G(253,121)=5,G(231,693)=-16.
解: , 如图1,建立平面直角坐标系,点P(x,0)是x轴上一点,则
可以看成点P与点A(0,1)的距离,
可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是求PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,所以PA′+PB的最小值为线段A′B的长度.为此,构造直角三角形A′CB,因为A′C=3,CB=3,所以 , 即原式的最小值为
.

根据以上阅读材料,解答下列问题: