 B .
B .  C .
C .  D .
D . 
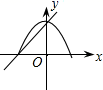 B .
B . 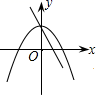 C .
C . 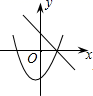 D .
D . 


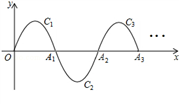
将C1绕点A1旋转180°得C2 , 交x轴于点A2;
将C2绕点A2旋转180°得C3 , 交x轴于点A3;
…
如此进行下去,直至得C13 . 若P(37,m)在第13段抛物线C13上,则m=.


①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,当x取何值时,商场获利润最大?
