一、选择题(本大题共有10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一项是符合题目要求的)
-
-
-
-
A . 1个
B . 2个
C . 3个
D . 4个
-
A . 相等的角是对顶角
B . 若 , 则
, 则 C . 两个锐角的和是钝角
D . 有两个角相等的三角形是等腰三角形
C . 两个锐角的和是钝角
D . 有两个角相等的三角形是等腰三角形
-
6.
(2024八上·邵阳期末)
北京市高级别自动驾驶示范区今年将启动

阶段建设,某区计划修建一条自动驾驶车道,在实际施工中,由于增加了施工人员,每天可以比原计划多修建50米,现在完成2500米与原计划完成2000米所用时间相同,设原计划每天修建车道
x米,根据题意可得方程( )
-
7.
(2024八上·邵阳期末)
已知

, 求作射线

平分

, 作法;

① 以O为圆心,适当长为半径作弧,交 于点M , 交
于点M , 交 于点N .
于点N .
② 分别以M , N为圆心.大于 的长为半径作弧,两弧在
的长为半径作弧,两弧在 的内部交于P .
的内部交于P .
③作射线 . 射线
. 射线 即为所求.请问作图依据是( )
即为所求.请问作图依据是( )
-
A . a<1
B . a>1
C . a<0
D . a>0
-
-
10.
(2024八下·冷水滩开学考)
如图,在

中,

,

平分

交

于点
D ,

平分

交

于点
E ,

,

交于点
F . 则下列说法正确的有( )
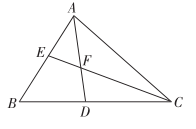
① ;②
;② ;③若
;③若 , 则
, 则 ;④
;④ .
.
A . 1个
B . 2个
C . 3个
D . 4个
二、填空题(本大题共有8个小题,每小题3分,共24分)
-
-
12.
(2024八上·邵阳期末)
某校组织八年级学生参观植物园时,了解到世界上最小的花粉是勿忘草的花粉,它的直径仅为

米,用科学记数法可表示为
米.
-
-
-
-
-
-
18.
(2024八上·邵阳期末)
疫情期间,有一批患者要入住邵阳市中心医院的某栋大楼,若每间住4人,则有38人无法入住;若每间住5人,则最后一间没住满.若设房间数为
x间,则可列不等式组为:
.
三、解答题(本大题共有8个小题,第19-25题每小题8分,第26题10分,共66分.解答应写出必要的文字说明、演算步骤或证明过程)
-
-
-
(1)
计算:

.
-
(2)
解分式方程:

.
-
-
-
23.
(2024八上·邵阳期末)
今年元旦节,某商场购进甲、乙两种纪念品,若购进甲种纪念品

件、乙种纪念品

件,则共需
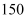
元,若购进甲种纪念品

件、乙种纪念品

件,则共需

元.
-
-
(2)
商场决定购进甲、乙两种纪念品共

件,若购进两种纪念品的总资金不超过

元,则最多购进甲种纪念品多少件?
-
-
25.
(2024八下·吉林月考)
阅读下列解题过程
例:若代数式 的值是2,求a的取值范围
的值是2,求a的取值范围
解:原式 ,
,
当 时,原式
时,原式 , 解得
, 解得 (舍去);
(舍去);
当 时,原式
时,原式 , 符合条件;
, 符合条件;
当 时,原式
时,原式 , 解得
, 解得 (舍去).
(舍去).
 的取值范围是
的取值范围是 .
.
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题:
-
(1)
当

时,化简:

.
-
(2)
若

, 求
a的取值范围.
-
-
(1)
求证:

;
-
(2)
用含

的式子表示

的度数;
-
(3)
如图2,当

时,取

,

的中点分别为点
P、
Q , 连接

,

,

, 判断

的形状,并加以证明.

于点M , 交
于点N .
的长为半径作弧,两弧在
的内部交于P .
. 射线
即为所求.请问作图依据是( )
的值是2,求a的取值范围
,
时,原式
, 解得
(舍去);
时,原式
, 符合条件;
时,原式
, 解得
(舍去).
的取值范围是
.