
 B .
B .  C .
C .  D .
D . 
日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期天 |
体温(℃) | 36.3 | 36.7 | 36.2 | 36.3 | 36.2 | 36.4 | 36.3 |
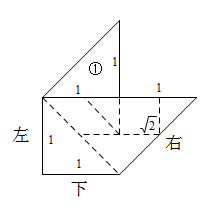

当时,如图1,抛物线
上的点
,
,
,
,
分别关于点
中心对称的点为
,
,
,
,
, 如下表:
… |
| … | ||||
… | … |
①补全表格:A ( ▲ , ▲)
②请在图1中描出表中对称后的点,再用平滑的曲线依次连接各点,得到的图象记为 .
①当时,若抛物线
与它的“孔像抛物线”
的函数值都随着
的增大而减小,则
的取值范围为 ▲;
②若二次函数及它的“孔像抛物线”与直线
有且只有三个交点,求
的值.
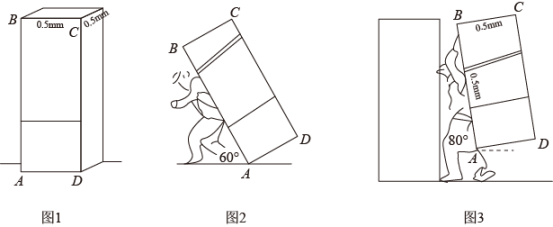
①四边形CEGF的形状是 ▲;
②的值为 ▲;
在图1的基础上,将正方形CEGF绕点C按顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;
如图3,在(2)的条件下,正方形CEGF 在旋转过程中,当B、E、F三点共线时,探究AG和GE的位置关系,并说明理由.
①当时,求
的面积
②当点P , Q运动至四边形为矩形时,请求出此时t的值.