广西壮族自治区三新学术联盟2023-2024学年高二上学期期...

更新时间：2024-03-12 浏览次数：16 类型：期末考试

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2024高二上·广西壮族自治区期末) 抛物线 $\text{[math]}$ 的焦点坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高二上·广西壮族自治区期末) 已知向量 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则z＝（）

A . ﹣4 B . 4 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高二上·广西壮族自治区期末) 设P是椭圆 $\text{[math]}$ 上的动点，则P到该椭圆的两个焦点的距离之和为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高二上·广西壮族自治区期末) 已知等差数列 $\text{[math]}$ 的前5项之和为25， $\text{[math]}$ ，则公差为（）

A . 6 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
5. (2024高二上·广西壮族自治区期末) 已知两直线 $\text{[math]}$ 与 $\text{[math]}$ 的交点在圆 $\text{[math]}$ 的内部，则实数k的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高二上·广西壮族自治区期末) 正项等比数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . 9 B . 72 C . 70 D . 48

答案解析收藏纠错 + 选题
7. (2024高二上·广西壮族自治区期末) 已知双曲线 $\text{[math]}$ ( $\text{[math]}$ )，以双曲线C的右顶点A为圆心，b为半径作圆A ，圆A与双曲线C的一条渐近线交于M ， N两点，若 $\text{[math]}$ ，则双曲线的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
8. (2024高二上·广西壮族自治区期末) 如图所示空间直角坐标系A﹣xyz中， $\text{[math]}$ 是正三棱柱 $\text{[math]}$ 的底面 $\text{[math]}$ 内一动点， $\text{[math]}$ ，直线PA和底面ABC所成的角为 $\text{[math]}$ ，则P点的坐标满足（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9. (2024高二上·广西壮族自治区期末) 若圆M： $\text{[math]}$ 与圆N： $\text{[math]}$ 相交，则k的取值可能为（）

A . $\text{[math]}$ B . 1 C . 3.8 D . 4.2

答案解析收藏纠错 + 选题
10. (2024高二上·广西壮族自治区期末) 关于x ， y的方程 $\text{[math]}$ 表示的曲线可以是（）

A . 椭圆 B . 双曲线 C . 抛物线 D . 圆

答案解析收藏纠错 + 选题
11. (2024高二上·广西壮族自治区期末) 已知 $\text{[math]}$ 是等差数列，其前n项和为 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论一定正确的有（）

A . $\text{[math]}$ B . $\text{[math]}$ 最小 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024高二上·广西壮族自治区期末) 如图，在长方体 $\text{[math]}$ 中，点P是底面 $\text{[math]}$ 内的动点，E ， F ， O ， K分别为AB ， BC ， BD ， $\text{[math]}$ 的中点，若 $\text{[math]}$ ，则下列说法正确的是（）

A . $\text{[math]}$ 的最大值为2 B . 三棱锥P﹣ABD的体积不变，表面积改变 C . 若 $\text{[math]}$ 平面 $\text{[math]}$ ，则 $\text{[math]}$ D . $\text{[math]}$ 的最小值为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分，共20分．

13. (2024高二上·广西壮族自治区期末) 若点 $\text{[math]}$ 在抛物线 $\text{[math]}$ 上，则该抛物线的方程为．

答案解析收藏纠错 + 选题
14. (2024高二上·广西壮族自治区期末) 已知空间向量 $\text{[math]}$ ， $\text{[math]}$ ，则向量 $\text{[math]}$ 在向量 $\text{[math]}$ 上的投影向量的坐标是．

答案解析收藏纠错 + 选题
15. (2024高二上·广西壮族自治区期末) 如图所示是一系列有机物的结构简图，途中的“小黑点”表示原子，两黑点间的“短线”表示化学键，按图中结构第n个图的化学键和原子的个数之和为个．(用含n的代数式表示)

答案解析收藏纠错 + 选题
16. (2024高二上·广西壮族自治区期末) 如图，棱长为1的正方体上有两个动点分别从顶点A ， C同时出发，以相同的速度1分别向点B ， D运动，最后同时到达，则在运动的过程中，两个动点间的最小距离为．

答案解析收藏纠错 + 选题

四、解答题：本题共6小题，共70分．解答应写出必要的文字说明、证明过程及演算步骤．

17. (2024高二上·广西壮族自治区期末) 在等比数列 $\text{[math]}$ 中，
1. （1）已知 $\text{[math]}$ ， $\text{[math]}$ ，求前4项和 $\text{[math]}$ ；
2. （2）已知公比 $\text{[math]}$ ，前6项和 $\text{[math]}$ ，求 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2024高二上·广西壮族自治区期末) 已知圆C经过 $\text{[math]}$ ， $\text{[math]}$ 两点，且圆心C在直线 $\text{[math]}$ 上．
1. （1）求圆C的方程；
2. （2）过点 $\text{[math]}$ 的直线l与圆C交于P ， Q两点，若 $\text{[math]}$ ，求直线l的方程．
答案解析收藏纠错 + 选题
19. (2024高二上·广西壮族自治区期末) 已知 $\text{[math]}$ 的周长为 $\text{[math]}$ ，其中点 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求点C的轨迹方程；
2. （2）设D为点A关于直线 $\text{[math]}$ 的对称点，求线段CD的长度的取值范围．
答案解析收藏纠错 + 选题
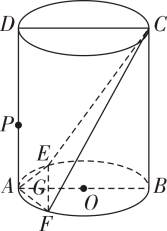
20. (2024高二上·广西壮族自治区期末) 如图，O是圆柱下底面的圆心，该圆柱的轴截面是边长为4的正方形ABCD ， P为线段AD上的动点，E ， F为下底面上的两点，且 $\text{[math]}$ ， $\text{[math]}$ ， EF交AB于点G ．
1. （1）当 $\text{[math]}$ 时，证明： $\text{[math]}$ 平面CEF；
2. （2）当 $\text{[math]}$ 为等边三角形时，求二面角 $\text{[math]}$ 的余弦值．
答案解析收藏纠错 + 选题
21. (2024高二上·广西壮族自治区期末) 已知过抛物线 $\text{[math]}$ 的焦点F ，斜率为2的直线交抛物线于A ， B两点，且 $\text{[math]}$ ．
1. （1）求抛物线的方程；
2. （2）抛物线的准线与x轴交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 的直线l交抛物线于M ， N两点，当 $\text{[math]}$ 时，求直线l的方程．
答案解析收藏纠错 + 选题
22. (2024高二上·广西壮族自治区期末) 已知数列 $\text{[math]}$ 是以公比为3，首项为3的等比数列，且 $\text{[math]}$ ．
1. （1）求出 $\text{[math]}$ 的通项公式；
2. （2）设 $\text{[math]}$ ，数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ，若不等式 $\text{[math]}$ 对任意的 $\text{[math]}$ 恒成立，求实数λ的取值范围．
答案解析收藏纠错 + 选题