吉林省长春市朝阳区2023-2024学年高二下学期开学考试数...

更新时间：2024-03-18 浏览次数：10 类型：开学考试

一、单选题（本题共8小题，每题5分 ，共40分。在每小题列出的选项中，选出符合题目的一项）

1. (2024高二下·朝阳开学考) 已知向量 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高二下·朝阳开学考) 在等比数列 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则公比 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高二下·朝阳开学考) 若直线经过点 $\text{[math]}$ 和圆C： $\text{[math]}$ 的圆心，并且与直线 $\text{[math]}$ 垂直，则m的值为（）

A . -4 B . 4 C . -1 D . 1

答案解析收藏纠错 + 选题
4. (2024高二下·朝阳开学考) 设点P，Q分别为直线 $\text{[math]}$ 与直线 $\text{[math]}$ 上的任意一点，则 $\text{[math]}$ 的最小值为（）

A . 1 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高二下·朝阳开学考) 设 $\text{[math]}$ 是等差数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高二下·朝阳开学考) 下列命题正确的个数是（）
①若A，B，C，D是空间任意四点，则有 $\text{[math]}$ = $\text{[math]}$
②若向量 $\text{[math]}$ 所在的直线为异面直线，则向量 $\text{[math]}$ 一定不共面
③若 $\text{[math]}$ 共线，则 $\text{[math]}$ 与 $\text{[math]}$ 所在直线平行
④对空间任意一点O与不共线的三点A、B、C，若 $\text{[math]}$ (其中x、y、z∈R)，则P、A、B、C四点共面

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
7. (2024高二下·朝阳开学考) 正方体 $\text{[math]}$ 的棱长为 $\text{[math]}$ 为棱 $\text{[math]}$ 中点， $\text{[math]}$ 为正方形 $\text{[math]}$ 内（舍边界）的动点，若 $\text{[math]}$ ，则动点 $\text{[math]}$ 的轨迹长度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高二下·朝阳开学考) 已知椭圆 $\text{[math]}$ 的左、右焦点分别为 $\text{[math]}$ 的上顶点为M，且 $\text{[math]}$ ，双曲线 $\text{[math]}$ 和椭圆 $\text{[math]}$ 有相同的焦点，P为 $\text{[math]}$ 与 $\text{[math]}$ 的一个公共点.若 $\text{[math]}$ （O为坐标原点），则 $\text{[math]}$ 的离心率 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题（本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题目要求。全部选对的得6分，有选错的得0分。若只有2个正确选顶，每选对一个得3分;若只有3个正确选项，每选对一个得2分。）

9. (2024高二下·朝阳开学考) 直线 $\text{[math]}$ ，圆 $\text{[math]}$ ，下列结论正确的是（）

A . 直线 $\text{[math]}$ 恒过定点 $\text{[math]}$ B . 直线 $\text{[math]}$ 与圆 $\text{[math]}$ 必有两个交点 C . 直线 $\text{[math]}$ 与圆 $\text{[math]}$ 的相交弦长的最大值为 $\text{[math]}$ D . 当 $\text{[math]}$ 时，圆 $\text{[math]}$ 上存在3个点到直线 $\text{[math]}$ 距离等于1

答案解析收藏纠错 + 选题
10. (2024高二下·朝阳开学考) 数列 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，都有 $\text{[math]}$ 恒成立，则（）

A . $\text{[math]}$ 为等差数列 B . $\text{[math]}$ 为等比数列 C . $\text{[math]}$ D . 实数 $\text{[math]}$ 的最小值为 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高二下·朝阳开学考) 已知抛物线 $\text{[math]}$ 的焦点为F，点P在抛物线上，点 $\text{[math]}$ ，点P到点Q和到y轴的距离分别为 $\text{[math]}$ ，则（）

A . 抛物线C的准线方程为 $\text{[math]}$ B . 若 $\text{[math]}$ ，则 $\text{[math]}$ 周长的最小值等于3 C . 若 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值等于2 D . 若 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值等于 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题（本题共3小题，每小题5分，共15分）

12. (2024高二下·朝阳开学考) 顶点在原点，焦点在y轴上，且过点 $\text{[math]}$ 的抛物线的标准方程是.

答案解析收藏纠错 + 选题
13. (2024高二下·朝阳开学考) 在正方体 $\text{[math]}$ 中，点E，F分别是底面 $\text{[math]}$ 和侧面 $\text{[math]}$ 的中心，若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024高二下·朝阳开学考) 已知 $\text{[math]}$ ，直线 $\text{[math]}$ 上存在点 $\text{[math]}$ ，满足 $\text{[math]}$ ，则实数 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题

四、解答题（本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤）

15. (2024高二下·丰城月考) 记 $\text{[math]}$ 为数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和.
1. （1）若 $\text{[math]}$ 为等差数列，且 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值；
2. （2）若 $\text{[math]}$ 为等比数列，且 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
16. (2024高二下·朝阳开学考) 已知椭圆 $\text{[math]}$ 的右焦点 $\text{[math]}$ 与抛物线 $\text{[math]}$ 的焦点重合，且椭圆的离心率为 $\text{[math]}$ .
1. （1）求椭圆 $\text{[math]}$ 的方程；
2. （2）过抛物线焦点的直线和抛物线相交于M，N两点， $\text{[math]}$ ，求直线方程.
答案解析收藏纠错 + 选题
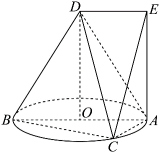
17. (2024高二下·朝阳开学考) 如图，在圆锥DO中，D为圆锥顶点，AB为圆锥底面的直径，O为底面圆的圆心，C为底面圆周上一点，四边形OAED为矩形．
1. （1）求证：平面BCD⊥平面ACE；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求平面ADE和平面CDE夹角的余弦值
答案解析收藏纠错 + 选题
18. (2024高二下·朝阳开学考) 已知双曲线 $\text{[math]}$ 的一条渐近线为 $\text{[math]}$ ，其虚轴长为 $\text{[math]}$ 为双曲线 $\text{[math]}$ 上任意一点．
1. （1）求双曲线的方程；
2. （2）求证： $\text{[math]}$ 到两条渐近线的距离之积为定值，并求出此定值；
3. （3）若双曲线 $\text{[math]}$ 的左顶点为 $\text{[math]}$ ，右焦点为 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题
19. (2024高二下·朝阳开学考) 已知数列 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ （ $\text{[math]}$ ）.
1. （1）求数列 $\text{[math]}$ 的通项 $\text{[math]}$ ；
2. （2）求数列 $\text{[math]}$ 的前n项和 $\text{[math]}$ ；
3. （3）若对于 $\text{[math]}$ ，使得 $\text{[math]}$ 恒成立，求实数 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题