一、单选题(本大题共10小题,每小题3分,共30分,每小题给出的四个选项中,只有一个是正确的)
-
-
A . 0
B . -1
C . -2
D . 2
-
-
-
5.
(2023八上·东西湖月考)
如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠BAE的大小为( )

A . 80°
B . 60°
C . 50°
D . 40°
-
A . 16
B . 25
C . 32
D . 64
-
A . -1
B . 5
C . -3
D . 1
-
-
A . -13
B . -4
C . -9
D . -5
-
10.
(2023八上·东西湖月考)
如图,

分别是边OA、OB上的定点,P、Q分别是边OB、OA上的动点,记


, 当

最小时,则关于

的数量关系正确的是( )

二、填空题:(本大题共6个小题,每小题3分,共18分)
-
-
-
-
-
-
16.
(2023八上·东西湖月考)
如图,等边三角形ABC中, BD⊥AC于D,BC=8,E在BD上一动点,以CE为边作等边三角形ECP,连DP,则DP的最小值为
.

三、解答题:(本大题共8个小题,共72分)
-
-
-
-
(1)
已知a+b=7,ab=10,求

,

的值;
-
(2)
先化简,再求值:

, 其中

.
-
-
(1)
若

, 求
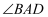
的度数;
-
(2)
求证:

是等腰三角形.
-
21.
(2023八上·东西湖月考)
如图是由边长为1的小正方形组成的6×7网格,每个小正方形的顶点叫做格点,△ABC和△DEF的顶点都是格点.

-
(1)
请在直线m上找到点P,使得PB+PC的值最小;
-
(2)
△ABC和△DEF关于直线n对称,请画出直线n;
-
-
-
22.
(2023八上·东西湖月考)
如图1,长方形的两边长分别为m+3,m+13;如图2的长方形的两边长分别为m+5,m+7.(其中m为正整数)

-
(1)
写出并计算两个长方形的面积

,

, 并比较

,

的大小;
-
(2)
现有一个正方形的周长与图1中的长方形的周长相等.试探究该正方形的面积与长方形的面积的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由;
-
(3)
在(1)的条件下,若某个图形的面积介于

、

之间(不包括

、

)且面积为整数,这样的整数有且只有19个,求m的值
-
23.
(2023八上·东西湖月考)
以△ABC的AB、AC为边作△ABD和△ACE,且AE=AB,AC=AD,CE与BD相交于M,∠EAB=∠CAD=α.

-
-
(2)
如图2,若G、H分别是EC、BD的中点,求∠AHG的度数(用含α式子表示);
-
(3)
如图3,连接AM,直接写出∠AMC与α的数量关系是.
-
24.
(2023八上·东西湖月考)
在平面直角坐标系中,已知点A(0,a),B(b,0),其中a,b满足:(x+b)(x+2)=x
2+ax+6(a,b为常数).
-
-
(2)
如图1,D为x轴负半轴上一点,C为第三象限内一点,且∠ABC=∠ADC=90°,AO=DO,DB平分∠ADC.过点C作CE⊥DB于点E,求证:DE=OB;
-
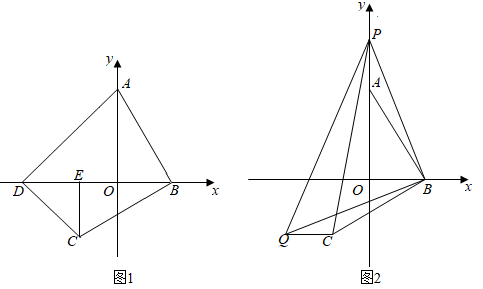
(3)
如图2,P为y轴正半轴上一动点,连接BP,过点B在x轴下方作BQ⊥BP,且BQ=BP,连接PC,PQ,QC.在(2)的条件下,设P(0,p),求△PCQ的面积(用含p的式子表示).





