贵州省黔东南州从江县东朗中学2023-2024学年九年级下学...

更新时间：2024-03-24 浏览次数：20 类型：开学考试

一、选择题:以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,每小题3分,共36分.

1. (2024九下·从江开学考) 已知☉O的半径为5 cm，圆心O到直线l的距离为5 cm，则直线l与☉O的位置关系为（）

A . 相交 B . 相切 C . 相离 D . 无法确定

答案解析收藏纠错 + 选题
2. (2024九下·从江开学考) 已知反比例函数的图象经过点(1，3)，则这个反比例函数的解析式为（）

A . y=- $\text{[math]}$ B . y= $\text{[math]}$ C . y= $\text{[math]}$ D . y=- $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·从江开学考) 一只小狗在如图所示的方砖上走来走去，若最终停在阴影方砖上，则甲胜，否则乙胜，那么甲的获胜概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九下·从江开学考) 若反比例函数y=(2m-1) $\text{[math]}$ 的图象在第二、第四象限，则m的值是（）

A . -1或1 B . 小于 $\text{[math]}$ 的任意实数 C . -1 D . 不能确定

答案解析收藏纠错 + 选题
5. (2024九下·从江开学考) 如图所示，反比例函数y= $\text{[math]}$ (x<0)与一次函数 y=x+4的图象交于A，B两点，A，B两点的横坐标分别为-3，-1.则关于x的不等式 $\text{[math]}$ <x+4(x<0)的解集为（）

A . x<-3 B . -3<x<-1 C . -1<x<0 D . x<-3或-1<x<0

答案解析收藏纠错 + 选题
6. (2024九下·从江开学考) 某闭合电路中，电源的电压为定值，电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间函数关系的图象，则用电阻R表示电流I的函数的解析式为（）

A . I= $\text{[math]}$ B . I= $\text{[math]}$ C . I= $\text{[math]}$ D . I=- $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·从江开学考) 如图所示，A是反比例函数y= $\text{[math]}$ (k≠0)图象上第二象限内的一点，AB⊥x轴，若△ABO的面积为2，则k的值为（）

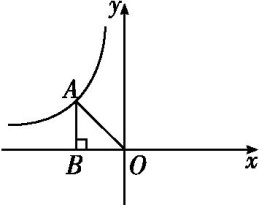
A . -4 B . -2 C . 2 D . 4

答案解析收藏纠错 + 选题
8. (2024九下·从江开学考) 如图所示，在△ABC中，∠C=90°，AC=4，BC=3.将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B，D两点间的距离为（）

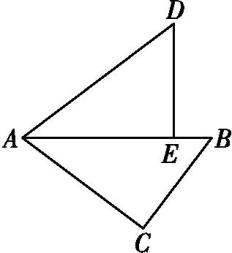
A . 2 $\text{[math]}$ B . $\text{[math]}$ C . 3 D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九下·从江开学考) 已知点A(-7，y₁)，B(-4，y₂)，C(5，y₃)在反比例函数y= $\text{[math]}$ (k>0)的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A . y₁<y₃<y₂ B . y₁<y₂<y₃ C . y₃<y₂<y₁ D . y₂<y₁<y₃

答案解析收藏纠错 + 选题
10. (2024九下·从江开学考) 如图所示的是三个反比例函数y= $\text{[math]}$ ， y= $\text{[math]}$ ， y= $\text{[math]}$ 在x轴上方的图象，由此观察得到k₁ ， k₂ ， k₃的大小关系是（）

A . k₁>k₂>k₃ B . k₃>k₂>k₁ C . k₂>k₃>k₁ D . k₃>k₁>k₂

答案解析收藏纠错 + 选题
11. (2024九下·从江开学考) 如图所示，在Rt△ABC中，∠C=90°，AC=6 cm，BC=2 cm，点P在边AC上，从点A向点C移动，点Q在边CB上，从点C向点B移动.若点P，Q均以1 cm/s的速度同时出发，且当一点移动到终点时，另一点也随之停止，连接PQ，则线段PQ的最小值是（）

A . 20 cm B . 18 cm C . 2 $\text{[math]}$ cm D . 3 $\text{[math]}$ cm

答案解析收藏纠错 + 选题
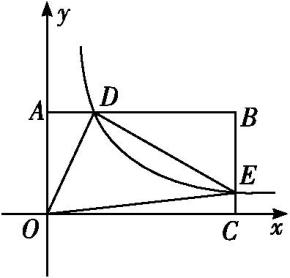
12. (2024九下·从江开学考) 如图所示，在以O为原点的平面直角坐标系中，矩形OABC的两边OC，OA分别在x轴、y轴的正半轴上，反比例函数y= $\text{[math]}$ (x>0)的图象与AB相交于点D，与BC相交于点E，若BD=3AD，且△ODE的面积是9，则k的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 12

答案解析收藏纠错 + 选题

二、填空题:每小题4分,共16分.

13. (2024九下·从江开学考) 在平面直角坐标系xOy中，若反比例函数y= $\text{[math]}$ (k≠0)的图象经过点A(1，2)和点 B(-1，m)，则m的值为.

答案解析收藏纠错 + 选题
14. (2024九下·从江开学考) 已知一个函数的图象与y= $\text{[math]}$ 的图象关于y轴对称，则该函数的解析式为.

答案解析收藏纠错 + 选题
15. (2024九下·从江开学考) 如图所示，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴、y轴的正半轴上，函数y= $\text{[math]}$ (k>0，x>0)交BC于点D，交AB于点E.若BD=2CD，S_{四边形ODBE}=4，则k的值为.

答案解析收藏纠错 + 选题
16. (2024九下·从江开学考) 如图所示，在平面直角坐标系中，正方形ABCD的顶点A，B分别在x轴、y轴上，对角线交于点E，反比例函数y= $\text{[math]}$ (x>0，k>0)的图象经过点C，E.若点A(3，0)，则k的值是.

答案解析收藏纠错 + 选题

三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.

17. (2024九下·从江开学考) 在面积为定值的一组矩形中，当矩形的一条边长为7.5 cm时，它的邻边长为8 cm.
1. （1）设矩形相邻的两条边长分别为x cm，y cm，求y关于x的函数解析式.这个函数是反比例函数吗?
2. （2）若其中一个矩形的一条边长为5 cm，求这个矩形与之相邻的另一条边长.
答案解析收藏纠错 + 选题
18. (2024九下·从江开学考) 已知反比例函数y= $\text{[math]}$ (k为常数，k≠0)的图象经过点A(2，3).
1. （1）求这个函数的解析式；
2. （2）当-3<x<-1时，直接写出y的取值范围；
3. （3）判断点B(-1，6)，C(3，2)是否在这个函数的图象上，并说明理由.
答案解析收藏纠错 + 选题
19. (2024九下·从江开学考) 如图所示，在平面直角坐标系中，点O为原点，反比例函数y= $\text{[math]}$ 的图象经过点(1，4)，菱形OABC的顶点A在函数的图象上，对角线OB在x轴上.
1. （1）求反比例函数的解析式；
2. （2）直接写出菱形OABC的面积.
答案解析收藏纠错 + 选题
20. (2024九下·从江开学考) 某校科技小组进行野外考察时，为了安全、迅速通过一片十几米宽的烂泥湿地，他们沿着前进路线用若干块木板铺了一条临时通道.木板对地面的压强 p(Pa)是木板面积S(m²)的反比例函数.
1. （1）求出此函数的解析式，并写出自变量取值范围；
2. （2）当木板面积为0.2 m²时，压强是；
3. （3）如果要求压强不超过6 000 Pa，木板的面积至少要多大?
答案解析收藏纠错 + 选题
21. (2024九下·从江开学考) 如图所示，在☉O中， $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ， OC与AD相交于点E.求证：
1. （1） AD∥BC；
2. （2）四边形BCDE为菱形.
答案解析收藏纠错 + 选题
22. (2024九下·从江开学考) 小聪在学习过程中遇到了一个函数 y= $\text{[math]}$ -2，小聪根据学习反比例函数y= $\text{[math]}$ 的经验，对函数y= $\text{[math]}$ -2的图象和性质进行了探究.他先通过列表，并描出如图所示的图象上的部分点.
1. （1）请你帮助小聪画出该函数的图象；
2. （2）该函数图象可以看成是由y= $\text{[math]}$ 的图象平移得到的，其平移方式为；
3. （3）直接写出不等式 $\text{[math]}$ -2>-3的解集为.
答案解析收藏纠错 + 选题
23. (2024九下·从江开学考) 为了预防疾病，某单位对办公室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y(mg)与时间x(min)成正比例，药物燃烧后，y与x成反比例(如图所示)，现测得药物8 min燃毕，此时室内空气中每立方米的含药量为6 mg，请根据题中所提供的信息，解答下列问题：
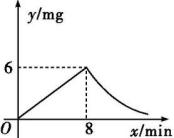
1. （1）药物燃烧时，求y关于x的函数解析式，自变量x的取值范围；药物燃烧后y关于x的函数解析式.
2. （2）研究表明，当空气中每立方米的含药量低于1.6 mg时员工方可进办公室，那么从消毒开始，至少经过几分钟后，员工才能回到办公室.
3. （3）研究表明，当空气中每立方米的含药量不低于3 mg且持续时间不低于10 min时，才能有效杀灭空气中的病菌，那么此次消毒是否有效?为什么?
答案解析收藏纠错 + 选题
24. (2024九下·从江开学考) 如图所示，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点(F不与A，B重合)，过点F的反比例函数y= $\text{[math]}$ (k>0)的图象与BC边交于点E.
1. （1）当F为AB的中点时，求该反比例函数的解析式；
2. （2）当k为何值时，△EFA的面积最大，最大面积是多少?
答案解析收藏纠错 + 选题
25. (2024九下·从江开学考) 试验数据显示，一般成人喝半斤低度白酒后，1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(小时)的关系可近似地用二次函数y=-200x²+400x刻画，1.5小时后(包括1.5小时)y与x可近似地用反比例函数y= $\text{[math]}$ (k>0)刻画(如图
所示).
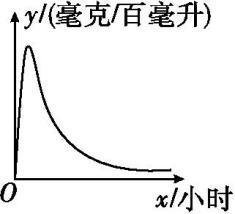
1. （1）根据上述数学模型计算：
  ①喝酒多长时间后血液中的酒精含量达到最大值?最大值为多少?
  ②求k的值.
2. （2）车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”，不能驾车上路.参照上述数学模型，假设某驾驶员晚上20：00在家喝完半斤低度白酒，第二天早上7：00能否驾车去上班?请说明理由.
答案解析收藏纠错 + 选题